Next: 9 Równanie Hamiltona-Jacobiego Up: Oscylator_harmoniczny_rozwiazanie Previous: 7 Metoda macierzowa
Hamiltonian oscylatora harmonicznego można zapisać w postaci:
Równania kanoniczne Hamiltona mają postać:
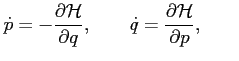
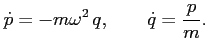
Znajdziemy transformację kanoniczną oryginalnego Hamiltonianu, prowadzącą do bardzo prostej postaci. Korzystając z jedynki trygonometrycznej, postulujemy transformację postaci:
Ponieważ transformacja nie zależy od czasu, nowy Hamiltonian ma postać po prostu równą:
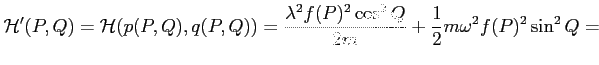
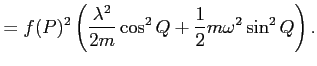
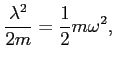 czyli
czyli
Obliczamy:
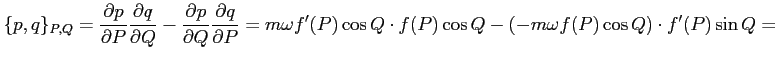
Aby tranformacja była kanoniczna, musi więc zachodzić:
Rozwiązujemy równanie różniczkowe na ![]() :
:
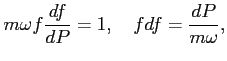
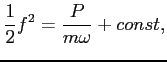
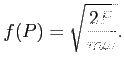
Nowym Hamiltonianem jest:
Równania kanoniczne przyjmują prostą postać:
Transformując z powrotem do funkcji ![]() otrzymujemy:
otrzymujemy:
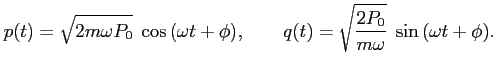
Warto zauważyć, że skoro ![]() jest Hamiltonianem,
to
jest Hamiltonianem,
to
![]() jest zachowaną energią, i wzór na
jest zachowaną energią, i wzór na ![]() jest identyczny wyprowadzonym wyżej wzorem (12) (
jest identyczny wyprowadzonym wyżej wzorem (12) (
![]() ).
).
2012-06-27