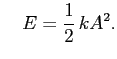Równanie (2) nie zawiera ,,czasu'' 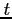 w sposób jawny. Oznacza to możliwość
obniżenia rzędu równania o jeden. Z fizycznego punktu widzenia w układzie (1)
jest zachowana energia. Mnożymy (1) przez
w sposób jawny. Oznacza to możliwość
obniżenia rzędu równania o jeden. Z fizycznego punktu widzenia w układzie (1)
jest zachowana energia. Mnożymy (1) przez 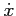 i przenosimy wszystkie składniki na lewą stronę:
i przenosimy wszystkie składniki na lewą stronę:
Całkujemy obustronnie po czasie (
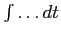 ):
):
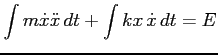 |
(10) |
gdzie wszystkie stałe całkowania zostały przeniesione na prawą stronę i oznaczone
literą 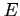 . Całki (10) są łatwe do obliczenia, pomimo że zawierają nieznaną (dowolną)
funkcję czasu
. Całki (10) są łatwe do obliczenia, pomimo że zawierają nieznaną (dowolną)
funkcję czasu 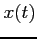 . W pierwszej stosujemy podstawienie
. W pierwszej stosujemy podstawienie
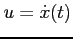 , a w drugiej
, a w drugiej 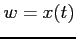 :
:
czyli:
Ostatecznie otrzymujemy:
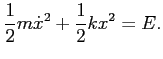 |
(11) |
Równanie (11) każdy fizyk powinien potrafić napisać natychmiast jako sumę energii kinetycznej i potencjalnej.
Wychodząc od (11) można rozwiązać (1). Przepisujemy (11)
podstawiając
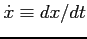 :
:
Powyższe jest równaniem o zmiennych rozdzielonych. Przenosimy wszystkie wyrazy zawierające 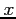 (w tym
(w tym 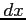 )
na lewą stronę, natomiast
)
na lewą stronę, natomiast 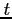 na prawą:
na prawą:
Całkujemy obustronnie:
Aby obliczyć całkę po prawej stronie przekształcamy:
Podstawiamy:
co daje:
Rozwiązanie ma postać (stała całkowania została oznaczona przez 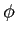 ):
):
Podstawiając
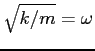 i
i
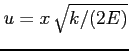 , dostajemy ostatecznie:
, dostajemy ostatecznie:
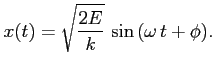 |
(12) |
Przy okazji dostajemy jako ,,bonus'' znany związek amplitudy drgań z energią:
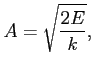
czyli:
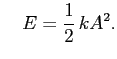
2012-06-27
![]() w sposób jawny. Oznacza to możliwość
obniżenia rzędu równania o jeden. Z fizycznego punktu widzenia w układzie (1)
jest zachowana energia. Mnożymy (1) przez
w sposób jawny. Oznacza to możliwość
obniżenia rzędu równania o jeden. Z fizycznego punktu widzenia w układzie (1)
jest zachowana energia. Mnożymy (1) przez ![]() i przenosimy wszystkie składniki na lewą stronę:
i przenosimy wszystkie składniki na lewą stronę:
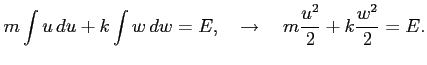
![]() :
:
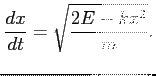
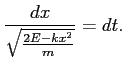
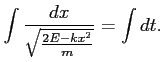
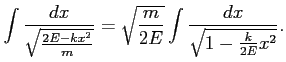
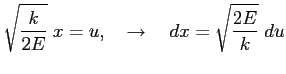
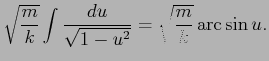
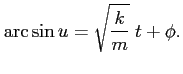
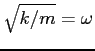 i
i
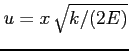 , dostajemy ostatecznie:
, dostajemy ostatecznie:
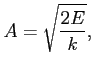 czyli:
czyli: