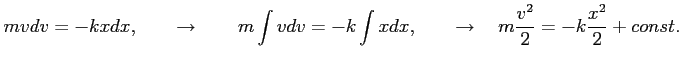4 Obniżenie rzędu równania

Przepisujemy równanie (1) wprowadzając prędkość $v=\dot{x}$:

$$m \frac{dv}{dt} = - k x.$$

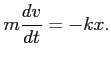
W powyższym równaniu dokonujemy zamiany zmiennej niezależnej, z $t$ na $x$:

$$\frac{dv}{dt} = \frac{dv}{dx} \cdot \frac{dx}{dt},$$

ale:

$$\frac{dx}{dt} = v,$$

i ostatecznie:

$$m v \frac{dv}{dx} = - k x.$$

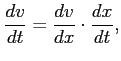
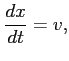
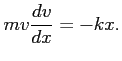
Otrzymaliśmy równanie pierwszego rzędu o zmiennych rozdzielonych:

$$m v dv = - k x dx, \qquad \to \qquad m \int v dv = -k \int x dx, \qquad \to \quad m \frac{v^2}{2} = -k \frac{x^2}{2} + const.$$

Dalszy sposób postępowania jest identyczny z przedstawionym poniżej równania (11).