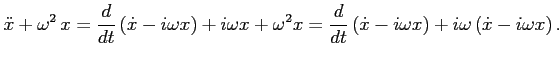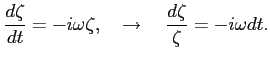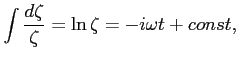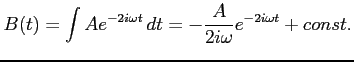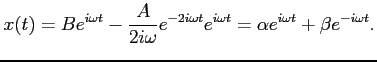Opisany sposób pochodzi od Landaua i Lifszyca .
Przekształcamy (2):
Podstawiamy za wyrażenia w nawiasach:
co daje:
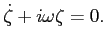 |
(13) |
Równanie (13) jest równaniem pierwszego rzędu o zmiennych rozdzielonych.
Jego rozwiązanie jest proste do uzyskania:
Całkując obustronnie otrzymujemy:
czyli:
Teraz musimy rozwiązać równanie niejednorodne:
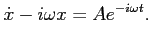 |
(14) |
Rozwiązanie równania (14) składa się z dwóch członów:
rozwiązania równania jednorodnego:
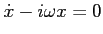 |
(15) |
i dowolnego (jakiegokolwiek) rozwiązania równania niejednorodnego (14).
Rozwiązanie (15) można uzyskać identycznie jak (13), co daje:
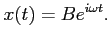 |
(16) |
Rozwiązanie r. niejednorodnego otrzymamy metodą uzmienniania stałych.
Zakładamy, że 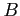 w (16) jest funkcją czasu
w (16) jest funkcją czasu
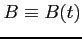 , i wstawiamy
do (14):
, i wstawiamy
do (14):
po uproszczeniu:
Całkując obustronnie ostatnie równanie po czasie dostajemy:
Stałą bierzemy równą zeru, bo interesuje nas jakiekolwiek rozwiązanie. Ostatecznie dostajemy:
gdzie podstawiłem
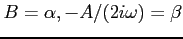 .
.
2012-06-27