Ogólna metoda rozwiązywania równań i układów liniowych równań różniczkowych zwyczajnych
opiera się o podstawienie:
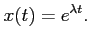 |
(6) |
Postawienie (6) sprowadza równanie różniczkowe do równania algebraicznego, które
daje tyle różnych3 wartości 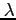 , ile wynosi rząd równania. Równania odpowiadające różnym
wartościom
, ile wynosi rząd równania. Równania odpowiadające różnym
wartościom 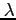 są liniowo niezależne, a rozwiązanie ogólne będzie miało postać:
są liniowo niezależne, a rozwiązanie ogólne będzie miało postać:
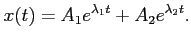 |
(7) |
Dla równania (2) procedura wygląda następująco. Obliczamy pierwszą i drugą pochodną:
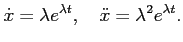 |
(8) |
Warto zauważyć, że różniczkowanie eksponenty sprowadza się w tym przypadku do mnożenia
przez 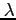 . Wstawiając (8) do (2) otrzymujemy:
. Wstawiając (8) do (2) otrzymujemy:
Z powyższego otrzymujemy równanie charakterystyczne o niewiadomej 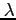 :
:
Jest to równanie kwadratowe z 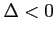 , posiadające dwa rozwiązania urojone:
, posiadające dwa rozwiązania urojone:
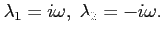 |
(9) |
Wstawiając (9) do (7) otrzymujemy rozwiązanie ogólne, identyczne z (3c).
2012-06-27