7 Metoda macierzowa

Rozwiązanie zagadnienia początkowego równania oscylatora harmonicznego można uzyskać sprowadzając problem do wektorowego równania liniowego pierwszego rzędu.

Zapisujemy (2) (używając podstawienia $\dot{x} = v$, tj. prędkości) jako układ r.r.liniowych I rzędu:

$$\begin{cases} \dot{x} = v \dot{v} = - \omega^2 x \end{cases}$$ (18)

lub równoważnie, w postaci macierzowej:

$$\frac{d}{dt} \left[ \begin{array}{c} x v \end{array} ... ...cdot \left[ \begin{array}{c} x v \end{array} \right].$$

Ponieważ rozwiązaniem równania:

$$\dot{y} = A y,$$

z warunkiem początkowym $y(0)=y_0$ jest:

$$y(t) = y_0 e^{A t},$$

analogicznie możemy poprawnie napisać rozwiązanie dowolnego układu r. liniowych I rzędu:

$$\dot{\mathbf{X}} = \mathbf{A} \cdot \mathbf{X}, \quad \math... ...t) \\ x_2(t) \\ \ldots \\ x_n(t) \end{array} \right].$$

Rozwiązanie zagadnienia początkowego $\mathbf{X}(0) = \mathbf{X}_0$ to:

$$\mathbf{X}(t) = e^{\mathbf{A} t} \cdot \mathbf{X}_0.$$

Dla oscylatora harmonicznego macierz $\mathbf{A}$ to:

$$\mathbf{A} = \left[ \begin{array}{cc} 0 & 1 \\ - \omega^2 & 0 \end{array} \right]$$

i głównym problemem staje się obliczenie wyrażenia:

$$e^{\left[ \begin{array}{cc} 0 & t \\ - \omega^2 t & 0 \end{array} \right]}$$

Obliczenie eksponenty macierzy jest możliwe z definicji:

$$e^{\mathbf{A}} = \sum_{n=0}^\infty \frac{1}{n!} \mathbf{A}^n$$

lub poprzez diagonalizację. Więcej szczegółów można znaleźć tutaj: [PDF].

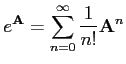
Wynik końcowy to:

$$e^{\mathbf{A} t} = \left[ \begin{array}{cc} \cos (\omega... ...ega \sin (\omega t) & \cos (\omega t) \end{array} \right],$$

a rozwiązanie równania oscylatora harmonicznego:

$$\left[ \begin{array}{c} x(t) v(t) \end{array} \righ... ...a t)} - x_0 \omega \sin{(\omega t)} \end{array} \right].$$