Next: About this document ... Up: Oscylator_harmoniczny_rozwiazanie Previous: 8 Przekształcenie kanoniczne
Rozwiązanie równań ruchu układu opisanego pewnym hamiltonianem, jest równoważne szukaniu rozwiązań (cząstkowego) równania Hamiltona-Jacobiego:
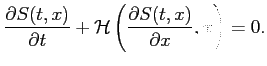
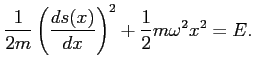
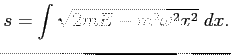
Całka jest typu:
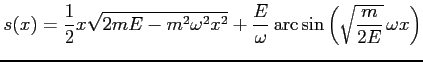
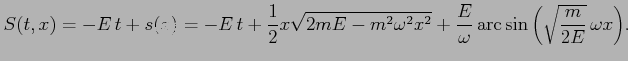
Zależność położenia od czasu jest wyznaczona w sposób uwikłany
pochodną czasową całki zupełnej względem energii ![]() :
:
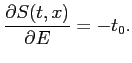
Obliczenie pochodnej cząstkowej po ![]() jest uciążliwe, ale ostatecznie wyrazy nie zawierające
jest uciążliwe, ale ostatecznie wyrazy nie zawierające
![]() upraszczają się:
upraszczają się:
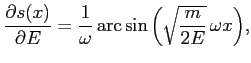
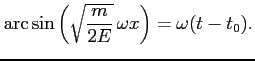
Działając obustronnie funkcją ![]() dostajemy:
dostajemy:
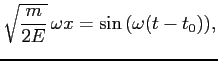
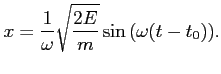
Końcowy wynik jest identyczny z (12), bo
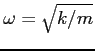 ).
).
Pochodna
![]() z kolei daje pęd:
z kolei daje pęd:
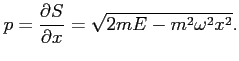
Warto zauważyć, że równanie Hamiltona-Jacobiego przypomina równanie Schrodingera,
natomiast stała ![]() określa translację w czasie, zgodnie z sensem zasady zachowania energii;
po energii
określa translację w czasie, zgodnie z sensem zasady zachowania energii;
po energii ![]() różniczkujemy całkę zupełną.
różniczkujemy całkę zupełną.
2012-06-27