

|
> Faculty of Physics, Astronomy and Applied Computer Science > Institute of Theoretical Physics > Department of Condensed Matter Theory and Nanophysics (ZTMSiN) > Prof. Adam Rycerz |
All my UJ pages > This site > Page for students (PL) > USOSweb > ZTMSiN Page > RUJ search
| Founding agency: | NCN (see the announcement) | |
| Principal investigator: | Dr. hab. Adam Rycerz | |
| Expected duration: | 2015 - 2020 |
|
Image adapted from Image library (The University of Manchester), with permission. [Click to enlarge.] |
The principal aim of the project to understand, by developing the theoretical description starting from the effective Dirac (or Dirac-Weyl) Hamiltonian, the selected phenomena in graphene (or other Dirac systems), belonging to the class of macroscopic quantum effects. Such effects, binding directly measurable material characteristics to fundamental constants and principles of quantum mechanics, offer powerful lenses through which to view the physics of condensed-matter systems, and are usually associated with exotic states of matter, such as superconductivity, superfluidity, or quantum Hall liquids in strong magnetic fields. Graphene, together with other Dirac systems or materials, in which effective quasiparticles follow the Dirac rather then the Schroedinger equation, have already provided quite a few novel examples of macroscopic quantum effects. These examples, surprizingly, have extended the collection of emergent phenomena in physics, as the systems build of nonrelativistic elements (e.g. carbon atoms at normal conditions) turns out to host relativistic quasiparticles.
In particular, we plan to focus on the macroscopic quantum effects in above-mentioned systems which were recently predicted theoretically but not confirmed experimentally as yet, first in order to learn whether the existing theoretical studies can be extended such that several factors (e.g. disorder, lattice deformations, electron-electron interaction) relevant in the actual experimental situations, are properly taken into account. Also, we would like to develop a complete theoretical description for some particular nanosystems, such as Dirac quantum dots with electron-electron interactions, which have not been studied in a rigorous manner so far.
The notion of emergent phenomena was coined out by P.W. Anderson in his milestone Science paper of 1979 [1]. In brief, emergence occurs when a complex system shows qualitatively different properties then its building blocks. Numerous examples of emergent systems studied in contemporary condensed matter physics, including high-temperature superconductors and heavy-fermion compounds [2], are regarded as systems with spontaneous symmetry breaking [3]. A link between emergence and spontaneous symmetry breaking, however, does not seem to have a permanent character. In a wide class of electronic systems, such as semiconducting heterostructures containing a two-dimensional electron gas (2DEG), physical properties of itinerant electrons are substantially different than properties of free electrons (or electrons in atoms composing the system), and are also highly-tunable upon variation of external electromagnetic fields [4]. To give some illustration of this tunability, we only mention that electrons in GaAs heterostructures can be usually described by a standard Schödinger equation of quantum mechanics with the effective mass $m_{\rm eff}=0.067\,m_e$ (where $m_e$ is the free electron mass), whereas in extreme cases of quantum states formed in quantum Hall systems, effective quasiparticles may not even show the Fermi-Dirac statistics [5,6].
It is rather rarely noticed that graphene, a two-dimensional form of carbon just one atom tick [7], also belongs to the second class of emergent systems (i.e., without an apparent spontaneous symmetry breaking) described briefly above. In a monolayer graphene, effective Hamiltonian for low-energy excitations has a Dirac-Weyl form, namely $$ {\cal H}_{\rm eff}= v_F\left[\,{\bf p}+e{\bf A}({\bf r},t)\,\right]\cdot{\bf\sigma}+U({\bf r},t), $$ where $v_F=10^6\,$m/s is the energy-independent Fermi velocity, ${\bf\sigma}=(\sigma_x,\sigma_y)$ with the Pauli matrices $\sigma_x$ and $\sigma_y$, ${\bf p}=-i\hbar(\partial_x,\partial_y)$ is the in-plane momentum operator, the electron charge is $-e$, and the external electromagnetic field is defined via scalar and vector potentials, $U({\bf r},t)$ and ${\bf A}({\bf r},t)$, with the in-plane position ${\bf r}=(x,y)$ and the time $t$. [Strictly speaking, the Hamiltonian ${\cal H}_{\rm eff}$ applies to quasiparticles near the $K$ valley in the dispersion relation. To obtain the effective Hamiltonian for other valley ($K'$) it is sufficient to substitute $\sigma_y\rightarrow{}-\sigma_y$.] In other words, the system build of nonrelativistic elements (carbon atoms at normal conditions) turns out to host ultrarelativistic quasiparticles, providing a beautiful example of an emergent phenomenon, which binds together two rather distant areas of relativistic quantum mechanics and condensed matter physics [8]. This observation applies generically to bilayer or multilayer graphenes [9], as well as to HgTe/CdTe quantum wells [10], although microscopic models describing such systems (hereinafter referred as other Dirac systems) are slightly different. It is also worth to mention so-called artificial graphenes: recently fabricated analogs of graphene, in which waves (of different kinds) obey their effective Dirac equations [11,12,13].
A peculiar nature of Dirac fermions in graphene originates from the chiral structure of the Hamiltonian ${\cal H}_{\rm eff}$, accompanied by the fact that coupling to the external electromagnetic field is described by additive terms, which are linear in both scalar and vector potentials. A remarkable consequence of these facts is the quantization of the visible light absorption [14], an unexpected macroscopic quantum effect recently found to have analogs in other Dirac systems [15,16], and even in a familiar graphite [17]. Another intriguing effect of this kind appears for dc conductivity of ballistic graphene [18]. In the so-called pseudodiffusive transport regime, the conductance of a rectangular sample (with the width $W$ and the length $L$) scales as $G=\sigma_0\times{}W/L$ for $W\gg{}L$, where $\sigma_0=(4/\pi)e^2/h$ is the universal quantum value of the conductivity [19,20], whereas the shot-noise power and all the other charge-transfer characteristics are indistinguishable from those of a classical diffusive conductor regardless the sample shape [21]. At high magnetic fields, the pseudodiffusive charge transport is predicted theoretically to reappear for resonances with Landau levels in both monolayer [22] and bilayer graphene [23]. In the presence of disorder, a fundamental property of the Hamiltonian - the time reversal symmetry (TRS) - starts to play a decisive role. In particular, effective TRS in a single valley may be broken even in the absence of magnetic fields, leading to observable (and having the universal character) consequences for the conductance and spectral fluctuations [24,25], as well as for the peculiar scaling behavior predicted for the conductivity [26,27].
Although the interest in graphene and other Dirac systems primarily focus on their potential applications [28,29], quite often linked to the nonstandard quantum description [30], we believe that the fundamental perspective sketched in the above also deserves a careful attention. In this project, we particularly intend to address the following questions arising from previous studies on the topic and not clearly answered as yet:
The above list is far from being complete, yet it provides some representative examples of specific research problems (research tasks) we plan to address in this project. In the remaining sections, we give some more specific description of each individual topic listed above.
One of the most unexpected properties of graphene, mentioned in previous section, is the pseudodiffusive nature of charge transport via undoped ballistic samples, manifesting itself by the fact that dc conductance obeys the Ohm’s law for classical conductors characterized by the universal quantum value of the conductivity. Such a macroscopic quantum phenomenon has a high-frequency analog, i.e., the visible opacity of graphene also takes quantized values [14]. However, the opacity directly scales with the number of graphene layers [17], yet such an additive property usually does not apply for dc conductance [9].
Early theoretical works on ballistic graphene bilayers [32,33] showed that the minimal conductivity at zero bias situation changes abruptly as a function of next-nearest neighbor interlayer hopping integral $t'$, taking the value of $\sigma_0=1/\pi$ [here we use the units of $8e^2/h$, which are most convenient in the bilayer case] for $t'=0$, or $\sigma_\star=3\sigma_0$ for any $t'\neq{}0$. Appearance of such a quantum critical behavior was attributed to the topological transition of the Fermi surface at low energies [9]. Experimental values of the minimal conductivity are generally lower than $\sigma_\star$, covering the range from $\sim\sigma_0$ [34] up to $2.5\,\sigma_0$ [35]. It was shown, employing the Landauer-Büttiker formalism, that the minimal conductivity of finite, ballistic samples is not universal but length-dependent [23], and can be rationalized, for large $L$, as $$ \sigma(L)\simeq\overline{\sigma}(L)=\sigma_\star \left[1-\left(\lambda/L\right)^\gamma\right], $$ where the characteristic length $\lambda=\lambda(t')$, and $\gamma<1$ is the parameter-independent exponent. In turn, the predictions of Refs. [32,33] are restored for $L\rightarrow\infty$, whereas in the opposite limit ($L\rightarrow{}0$) one gets $\sigma(L)\rightarrow\sigma_0$ regardless $t'=0$ or $t'\neq{}0$. It is also shown in Ref. [23] that the universal conductivity is restored for resonances with the Landau levels at high magnetic fields. We further notice that some numerical studies of disordered monolayer samples report the longitudinal conductivity close to $\sigma_0$, appearing at each Landau level for wide ranges of disorder and magnetic fields [36].
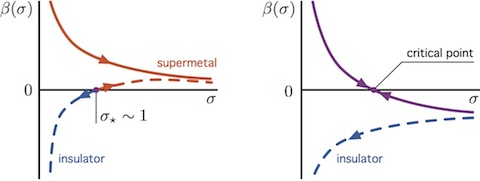
Very recently, Rut and the author [31] pointed out that the scaling function $$ \beta(\sigma)=\frac{d\ln\!\sigma}{d\ln\!L}, $$ which plays a central role in conceptual understanding of the metal insulator transition [37] and is widely-considered in the context of disordered Dirac or spin-orbit systems [26,27,38,39] (see the figure below), also unveils an intriguing analogy between interaction-induced quantum criticality in disordered Dirac systems [27] and transport properties of ballistic graphene bilayer with skew interlayer hoppings.
|
Schematic scaling functions $\beta(\sigma)$ for two-dimensional disordered Dirac (solid lines) and spin-orbit (dashed lined) systems. Left: noninteracting case [26,38], right: Coulomb interaction included [27]. Arrows indicate the flows of the dimensionless conductivity $\sigma$ with increasing $L$. (Adapted from Ref. [27].) [Click to enlarge.] |
In brief, the scaling function $\beta(\sigma)$ can be obtained by numerical differentiation of $\sigma(L)$ resulting from the mode-matching analysis. For the asymptotic range, this leads to $$ \beta(\sigma)\simeq{} -\gamma\left( 1-\sigma_\star/\sigma \right), $$ with $\sigma=\sigma_\star\simeq{}3/\pi$ being an attractive fixed point [$\beta'(\sigma_\star)<0$ for $\gamma\simeq{}1/2>0$] of the renormalization group flow. Such a scenario, earlier predicted for disordered Dirac systems with Coulomb interaction [27], is reproduced by our results for graphene bilayer. The values of $\beta(\sigma)$ obtained numerically become $t'$-independent and follow the above approximating formula for $\sigma\gtrsim{}0.8$.
This surprising coincidence (it is worth to stress here that the system considered was ballistic and no interactions were taken into account) seems difficult to understand in terms of existing symmetry-based theory of localization [27, 39]. Particular features of the results suggest that next-nearest neighbor interlayer hoppings, apart from breaking the rotational symmetry of the Hamiltonian in a single valley (a phenomenon know as trigonal warping [9]), may also induce corrections to $\beta(\sigma)$ of the Altshuler-Aronov type [40], destroying the so-called supermetallic phase in graphene.
It would be very beneficial to further clarify of the above-mentioned issue. This requires numerical study of charge transport through the disordered graphene bilayer, which constitutes the first research task of this project. In particular, we intend to perform extensive numerical simulations of electron transport for at least two different models of disordered bilayer: the well-known tight-binding model on a honeycomb lattice, as well as the complementary model based on the direct discretization of the effective Dirac equation [41]. We believe, that such a comparative study shall determine the role of disorder-induced intervalley scattering, which may restore the time-reversal symmetry. Furthermore, we wish to find out whether the attractive fixed point at $\sigma=\sigma_\star\simeq{}3/\pi$ is affected or not by different possible types of disorder in graphene bilayer (e.g.\ potential disorder or gap-disorder). It seems also intriguing if the disorder may lead to a renormalization-group flow approaching the fixed point $\sigma_\star$ from the bottom, i.e., taking $\beta(\sigma)<0$ values; a part of the picture which is obviously missing in a ballistic system.
Dirac fermions confined in graphene quantum dots [42] have provided yet another surprising situation, in which a piece of handbook knowledge needed a careful revision.
Quantum chaotic behavior appears generically for systems, whose classical dynamics are chaotic, and manifests itself via the fact that energy levels show statistical fluctuations following those of Gaussian ensembles of random matrices [43]. In particular, if such a system posses the time-reversal symmetry (TRS), its spectral statistics follow the Gaussian orthogonal ensemble (GOE). A system with TRS and half-integer spin has the symplectic symmetry and, in turn, shows spectral fluctuations of the Gaussian symplectic ensemble (GSE). If TRS is broken, as in the presence of nontrivial gauge fields, and the system has no other antiunitary symmetry [44], spectral statistics follow the Gaussian unitary ensemble (GUE). For a particular case of massless spin-1/2 particles, it was pointed out by Berry and Mondragon [45], that the confinement may break TRS in a persistent manner (i.e., even in the absence of gauge fields), leading to the spectral fluctuations of GUE.
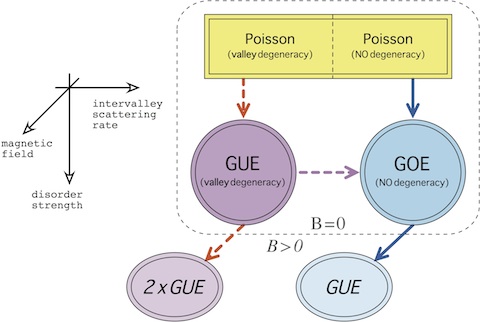
When applying the above symmetry classification to graphene nanosystems [24, 25] one needs, however, to take into account that Dirac fermions in graphene appear in the two valleys, $K$ and $K'$, coupled by TRS. [In particular, real magnetic field break TRS and has the same sign in the two valleys, whereas the strain-induced gauge field preserves TRS and has opposite signs in the two valleys.] If the valley pseudospin is conserved, a special (symplectic) time-reversal symmetry (STRS) becomes relevant, playing a role of an effective TRS in a single valley [24]. Both real magnetic and strain-induced gauge fields may break STRS leading to the spectral fluctuations of GUE. As demonstrated numerically in Ref. [25], such fluctuations also appear for particular closed nanosystems in graphene in the presence of random scalar potentials slowly varying on the scale of atomic separation. Such nanosystems include equilateral triangles with zigzag or Klein edges, i.e., with terminal atoms belonging to one sublattice. Generic graphene nanoflakes with irregular edges show spectral fluctuations of GOE [24], as strong intervalley scattering restores TRS in the absence of gauge fields (see the figure below). In contrast, the boundary effects are suppressed in open graphene systems, for which signatures of the symplectic symmetry class were reported [46].
|
Transitions between symmetry classes and random matrix ensembles relevant for closed nanosystems in graphene characterized by the disorder strength, the intervalley scattering rate, and (optionally) placed in the weak magnetic field $B$. Solid arrows in the right part indicate transitions reported in the literature prior to Ref. [25]; dashed arrows indicate remaining transitions. [Click to enlarge.] |
Although the issue of quantum chaos in graphene nanosystems has been reworked quite extensively from the theoretical side, a few open problems remains. We are particularly interested in spectral fluctuations appearing a situation, when terminal atoms belongs predominantly to one sublattice, but the edges are not oriented precisely along a zigzag direction, what constitutes the second research task of the project.
It is worth mention here, that triangular graphene flakes, similar to studied theoretically in Ref. [25], have been recently fabricated [47, 48]. However, due to the hybridization with metallic substrates, quantum-dot energy levels in such systems are significantly broaden, making it impossible to determine the symmetry class via spectral statistics. This obstacle seems to be of an irreducible nature, motivating one to search for new theoretical tools, as none of the well-established symmetry classifications build on spectral [43] and conductance fluctuations [49] can be directly employed. This is because in the experimental situation of Refs. [47, 48] the metallic substrate plays a role one lead, well-connected to the graphene nanostructure. The other lead is replaced by the STM tip, providing only a tunneling contact, which probes the local density of states in the nanostructure. We hope one of nonstandard characteristics, considered in theoretical description of quantum chaotic systems [43], will help to rationalize the experimental data also in the energy range when transmission resonances associated with individual levels start to overlap.
There was a long debate whether strong electron correlations may manifest itself in graphene or other Dirac systems, as the viral theorem implies the absence of Wigner crystallization in such systems [50]. It has become clear, since the experimental demonstration of the long-range magnetic order in functionalized graphene by Hong et al. [51] (preceded by several theoretical works, see Ref. [52]) that strong correlations may appear in various situations, when local electronic structure is modified due to impurities, defects, lattice termination, etc., compelling one to go beyond the Dirac Hamiltonian in quantum-mechanical description of the system.
In this part of the project, we plan to focus on slightly different physical situations, when the Hamiltonian ${\cal H}_{\rm eff}$, supplemented with the mass term if necessary, provides a correct single-particle description, but quantum critical behaviors may emerge from other reasons. For instance, in graphene quantum dots, the energy spectrum is discrete and the substrateinduced mass term may appear [53]. In a such situation, the results of Ref. [50] are no longer relevant. For Dirac nanosystems, the systematic analysis of correlated states is generally difficult, due to an unbounded single-particle spectrum [54]. Exact numerical solutions for small, isolated clusters of a honeycomb lattice exhibit some signatures of the so-called spin liquid phase [55], an exotic quantum state having no analog in corresponding Schrödinger systems. Although the model parameters, for which spin liquid is predicted to appear, are rather distant from interaction strengths in natural Dirac systems such as graphene, they seem possible to reproduce in artificial systems [11]. (However, the later numerical study by Sorella et al. [56] put the existence of the spin liquid phase in question.)
We believe it would be beneficial to reconsider the issues sketched above focusing on Dirac quantum dots (DQD) in a continuous limit. Our third research task starts from the discussion of single-particle quantum states, which can be found analytically for DQD of some particular shapes, or numerically for arbitrary shapes [45]. Having the single particle basis, one can determine the matrix elements of the interaction Hamiltonian, and find an approximated solution the resulting manybody problem using one of the standard techniques. The resulting multiparticle wavefunction can then be improved variationally via the single-particle basis renormalization, in a framework similar to the so-called exact diagonalization - ab initio (EDABI) approach to strongly correlated electron systems [57]. In such an approach, putting equal footing on single- and multiparticle aspect of the problem, the formal unboundness of the energy spectrum should not affect the numerical stability, at least for the systems with discrete energy spectra and nonzero mass term. Of course, this particular supposition needs to be carefully verified by analysing the standard signatures of numerical convergence as functions of the system size, the mass gap, and other physical parameters. Apart from the technical aspects, we plan to put a particular emphasis on the wavefunction localization and the magnetic properties (i.e., the competition between the antiferromagnetic coupling for localized states and the Hunds rule for extended states). The possible relation between these aspects of many-body quantum physics and the character of classical system dynamics (which can be integrable or chaotic) will also be studied.
Macroscopic quantum effects, binding directly measurable material characteristics to fundamental constants and principles of quantum mechanics, offer powerful lenses through which to view the physics of condensed-matter systems. Graphene, together with other Dirac materials, in which effective quasiparticles follow the Dirac (or Dirac-Weyl) rather then the Schrödinger equation, have already provided a few examples of such unique phenomena. The principal purpose of this project is to understand selected phenomena of this class, which were recently predicted theoretically but not (or not fully) confirmed experimentally as yet.
| [1] | P.W. Anderson, More is different, Science 177, 393-396 (1972). |
| [2] | J. Spałek, Correlated fermions: a new paradigm in physics on the example of solid state physics, Eur. J. Phys. 21, 511-534 (2000). |
| [3] | P.W. Anderson, Basic notions of Condensed Matter Physics, Addison-Wesley (Reading, 1997). |
| [4] | C.W.J. Beenakker and H. van Houten, Quantum Transport in Semiconductor Nanostructures, Solid State Physics 44, 1-228 (1991); e-print arXiv:cond-mat/0412664. |
| [5] | A. Stern, Non-Abelian states of matter, Nature 464, 187-193 (2010). |
| [6] | R.L. Willett, C. Nayak, L.N. Pfeiffer, and K.W. West, Magnetic field-tuned Aharonov-Bohm oscillations and evidence for non-Abelian anyons at $\nu = 5/2$, Phys. Rev. Lett. 111, 186401 (2013). |
| [7] | M.I. Katsnelson, Graphene: Carbon in Two Dimensions, Cambridge University Press (Cambridge, 2012). |
| [8] | D.S.L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler, and T. Chakraborty, Properties of Graphene: A Theoretical Perspective, Advances in Physics 59, 261-462 (2010). |
| [9] | E. McCann and M. Koshino, The electronic properties of bilayer graphene, Rep. Prog. Phys. 76, 056503 (2013) pp. 1-28. |
| [10] | B.A. Bernevig, T.L. Hughes, and S.C. Zhang, Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells, Science 314, 1757-1761 (2006). |
| [11] | A. Singha, M. Gibertini, B. Karmakar, S. Yuan, M. Polini, G. Vignale, M.I. Katsnelson, A. Pinczuk, L.N. Pfeiffer, K.W. West, and V. Pellegrini, Two-Dimensional Mott-Hubbard Electrons in an Artificial Honeycomb Lattice, Science 332, 1176–1179 (2011). |
| [12] | D. Torrent and J. Sánchez-Dehesa, Acoustic Analogue of Graphene: Observation of Dirac Cones in Acoustic Surface Waves, Phys. Rev. Lett. 108, 174301 (2012). |
| [13] | [13] K.K. Gomes, W. Mar, W. Ko, F. Guinea, and H.C. Manoharan, Designer Dirac fermions and topological phases in molecular graphene, Nature 483, 306–310 (2012). |
| [14] | R.R. Nair, P. Blake, A.N. Grigorenko, K.S. Novoselov, T.J. Booth, T. Stauber, N.M.R. Peres, and A.K. Geim, Universal Dynamic Conductivity and Quantized Visible Opacity of Suspended Graphene, Science 320, 1308 (2008). |
| [15] | J. Maciejko, X.-L. Qi, H.D. Drew, and S.-C. Zhang, Topological Quantization in Units of the Fine Structure Constant, Phys. Rev. Lett. 105, 166803 (2010). |
| [16] | A.M. Shuvaev, G.V. Astakhov, G. Tkachov, C. Brüne, H. Buhmann, L.W. Molenkamp, and A. Pimenov, Terahertz quantum Hall effect of Dirac fermions in a topological insulator, Phys. Rev. B 87, 121104(R) (2013). |
| [17] | H.S. Skulason, P.E. Gaskell, and T. Szkopek, Optical reflection and transmission properties of exfoliated graphite from a graphene monolayer to several hundred graphene layers, Nanotechnology 21, 295709 (2010). |
| [18] | S. Das Sarma, Sh. Adam, E.H. Hwang, and E. Rossi, Electronic transport in twodimensional graphene, Rev. Mod. Phys. 83, 407–470 (2011). |
| [19] | J. Tworzydło, B. Trauzettel, M. Titov, A. Rycerz, and C.W.J. Beenakker, Sub-Poissonian Shot Noise in Graphene, Phys. Rev. Lett. 96, 246802 (2006). |
| [20] | R. Danneau, F.Wu, M.F. Craciun, S. Russo, M.Y. Tomi, J. Salmilehto, A.F. Morpurgo, and P.J. Hakonen, Shot Noise in Ballistic Graphene, Phys. Rev. Lett. 100, 196802 (2008). |
| [21] | A. Rycerz, P. Recher, and M. Wimmer, Conformal mapping and shot noise in graphene, Phys. Rev. B 80, 125417 (2009). |
| [22] | E. Prada, P. San-Jose, B. Wunsch, and F. Guinea, Pseudodiffusive magnetotransport in graphene, Phys. Rev. B 75, 113407 (2007). |
| [23] | G. Rut and A. Rycerz, Pseudodiffusive conductance, quantum-limited shot noise, and Landau-level hierarchy in biased graphene bilayer, Phys. Rev. B 89, 045421 (2014). |
| [24] | J. Wurm, A. Rycerz, I. Adagideli, M. Wimmer, K. Richter, and H.U. Baranger, Symmetry Classes in Graphene Quantum Dots: Universal Spectral Statistics, Weak Localization, and Conductance Fluctuations, Phys. Rev. Lett. 102, 056806 (2009). |
| [25] | A. Rycerz, Random matrices and quantum chaos in weakly-disordered graphene nanoflakes, Phys. Rev. B 85, 245424 (2012). |
| [26] | J.H. Bardarson, J. Tworzydło, P.W. Brouwer, and C.W.J. Beenakker, One-Parameter Scaling at the Dirac Point in Graphene, Phys. Rev. Lett. 99, 106801 (2007). |
| [27] | P.M. Ostrovsky, I.V. Gornyi, and A.D. Mirlin, Interaction-Induced Criticality in Z2 Topological Insulators, Phys. Rev. Lett. 105, 036803 (2010). |
| [28] | A.K. Geim and P. Kim, Carbon Wonderland, Scientific American (April 2008). |
| [29] | A.K. Geim, Graphene: Status and Prospects, Science 324, 1530–1534 (2009). |
| [30] | A. Rycerz, Graphene: The Future of Electronics Lies in Quantum Theory, published online at www.atomiumculture.eu (2014). |
| [31] | G. Rut and A. Rycerz, Minimal conductivity and signatures of quantum criticality in ballistic graphene bilayer, Europhys. Lett. 107, 47005 (2014). |
| [32] | I. Snyman and C.W.J. Beenakker, Ballistic transmission through a graphene bilayer, Phys. Rev. B 75, 045322 (2007). |
| [33] | J. Cserti, A. Csordás, and G. Dávid, Role of the Trigonal Warping on the Minimal Conductivity of Bilayer Graphene, Phys. Rev. Lett. 99, 066802 (2007). |
| [34] | B. Feldman, J. Martin, and A. Yacoby, Broken-symmetry states and divergent resistance in suspended bilayer graphene, Nature Phys. 5, 889-893 (2009). |
| [35] | A.S. Mayorov, D.C. Elias, M. Mucha-Kruczyński, R.V. Gorbachev, T. Tudorovskiy, A. Zhukov, S.V. Morozov, M.I. Katsnelson, V.I. Fal’ko, A.K. Geim, and K.S. Novoselov, 13 Interaction-Driven Spectrum Reconstruction in Bilayer Graphene, Science 333, 860-863 (2011). |
| [36] | F. Ortmann and S. Roche, Splitting of the Zero-Energy Landau Level and Universal Dissipative Conductivity at Critical Points in Disordered Graphene, Phys. Rev. Lett. 110, 086602 (2013). |
| [37] | K. Efetov, Supersymmetry in Disorder and Chaos (Cambridge University, Cambridge, 1997). |
| [38] | K. Nomura, M. Koshino, and S. Ryu, Topological Delocalization of Two-Dimensional Massless Dirac Fermions, Phys. Rev. Lett. 99, 146806 (2007). |
| [39] | F. Evers and A.D. Mirlin, Anderson transitions, Rev. Mod. Phys. 80, 1355 (2008). |
| [40] | B.L. Altshuler and A.G. Aronov, in Electron-Electron Interactions in Disordered Conductors, edited by A.L. Efros and M. Pollak (Elsevier, New York, 1985), p. 1. |
| [41] | M.V. Medvedyeva, On localization of Dirac fermions by disorder, Doctoral Thesis (Leiden University, 2011); http://hdl.handle.net/1887/17606. |
| [42] | L.A. Ponomarenko, F. Schedin, M.I. Katsnelson, R. Yang, E.W. Hill, K.S. Novoselov, and A.K. Geim, Chaotic Dirac Billiard in Graphene Quantum Dots, Science 320, 356-358 (2008). |
| [43] | F. Haake, Quantum Signatures of Chaos, 3rd ed. (Springer, Berlin, 2010). |
| [44] | M. Robnik and M.V. Berry, False time-reversal violation and energy level statistics: the role of anti-unitary symmetry, J. Phys. A: Math. Gen. 19, 669-682 (1986). |
| [45] | M.V. Berry and R.J. Mondragon, Neutrino billiards: time-reversal symmetry-breaking without magnetic fields, Proc. R. Soc. A 412, 53-74 (1987). |
| [46] | A.N. Pal, V. Kochat, and A. Ghosh, Direct Observation of Valley Hybridization and Universal Symmetry of Graphene with Mesoscopic Conductance Fluctuations, Phys. Rev. Lett. 109, 196601 (2012). |
| [47] | S.K. Hämäläinen, Z. Sun, M.P. Boneschanscher, A. Uppstu, M. Ijäs, A. Harju, D. Vanmaekelbergh, and P. Liljeroth, Quantum-Confined Electronic States in Atomically Well- Defined Graphene Nanostructures, Phys. Rev. Lett. 107, 236803 (2011). |
| [48] | M. Olle, G. Ceballos, D. Serrate, and P. Gambardella, Yield and Shape Selection of Graphene Nanoislands Grown on Ni(111), Nano Lett. 12, 4431 (2012). |
| [49] | C.W.J. Beenakker, Random Matrix Theory of Quantum Transport, Rev. Mod. Phys. 69, 731-808 (1997). |
| [50] | J.D. Stokes, H.P. Dahal, A.V. Balatsky, and K.S. Bedell, The Virial Theorem in Graphene and other Dirac Materials, Philos. Mag. 93, 672-679 (2013). |
| [51] | J. Hong, E. Bekyarova, W.A. de Heer, R.C. Haddon, and S. Khizroev, Chemically Engineered Graphene-Based 2D Organic Molecular Magnet, ACS Nano 7, 10011-10022 (2013). |
| [52] | O.V. Yazyev, Emergence of magnetism in graphene materials and nanostructures, Rep. Prog. Phys. 73 056501 (2010). |
| [53] | K.A. Guerrero Becerra and M. Rontani, Wigner Localization in a Graphene Quantum Dot with a Mass Gap, Phys. Rev. B 90,125446 (2014). |
| [54] | W. Häusler and R. Egger, Artificial atoms in interacting graphene quantum dots, Phys. Rev. B 80, 161402(R) (2009). |
| [55] | Z.Y. Meng, T.C. Lang, S. Wessel, F.F. Assaad, and A. Muramatsu, Quantum spin liquid emerging in two-dimensional correlated Dirac fermions, Nature 464, 847–851 (2010). |
| [56] | S. Sorella, Y. Otsuka, and S. Yunoki, Absence of a Spin Liquid Phase in the Hubbard Model on the Honeycomb Lattice, Scientific Reports 2, 992 (2012). |
| [57] | J. Spałek, E.M. Görlich, A. Rycerz, and R. Zahorbeński, The combined exact diagonalization - ab initio approach and its application to correlated electronic states and Mott- Hubbard localization in nanoscopic systems, J. Phys. Condens. Matter 19, 255212 (2007) pp. 1-43. |