Cóż może być prostszego od numerycznego obliczenia pochodnej funkcji zadanej prostą całką? Na dodatek mówimy o wartości tej pochodnej w JEDNYM punkcie, i możemy na to poświęcić wiele godzin pracy (super)komputera. Jeżeli ktoś zgadza się, że to trywialne zadanie, sugeruję obliczenie trzeciej pochodnej po eta relatywistycznej całki Fermiego-Diraca dla k=1/2, eta=64 oraz theta=2^38 = 2.74877906944000000000e11. Właściwie już ustalenie jej znaku należałoby uznać za sukces...

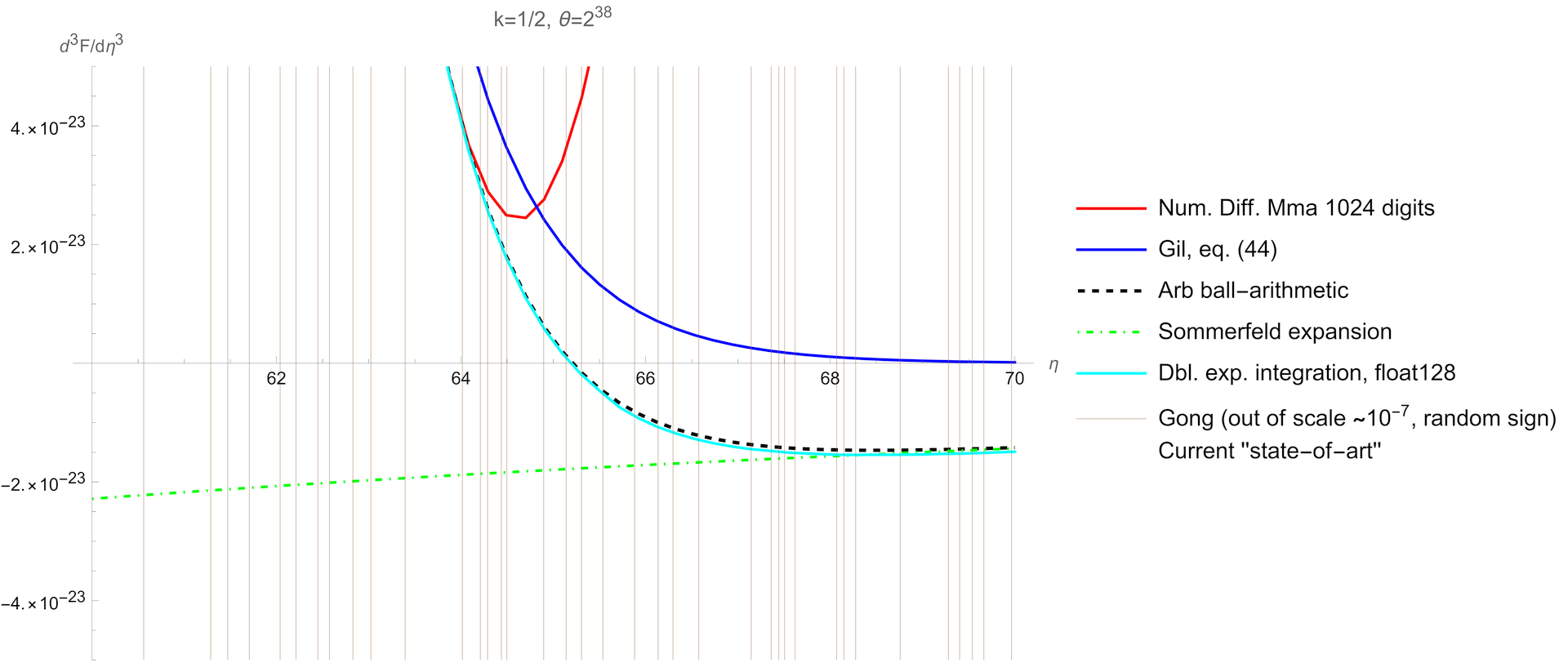
Problem doskonale ilustruje poniższy wykres.

Już pierwszy rzut oka na powyższy wykres unaocznia problem. Każda metoda produkuje inny wynik, różnice są drastyczne. Powszechnie używana w astrofizyce metoda, czyli rozbicie przedziału całkowania i zastosowanie kwadratury Gaussa (200-punktowej!) na początku przedziału oraz Gaussa-Laguerra na zanikającym wykładniczo ,,ogonie'' daje katastrofalnie błędne wyniki pokazane cienką brązową linią. Algorytm z pracy Gong et. al. (2001) produkuje losowe liczby rzędu 1e-7, wyskakujące poza skalę wykresu o kilkanaście rzędów wielkości. Podobnie nonsensowne wyniki produkuje uznany za inżynieryjny standard algorytm integral programu MATLAB R2021a. Pozostałe wyniki, z których każdy można uznać za state-of-art w 2022 roku, nie są już losowe, ale oczywiście nie mogą być wszystkie poprawne! Opiszę je po kolei.

Pierwsza metoda (czerwona linia), to użycie brutalnej siły programu Mathematica, czyli NIntegrate z użyciem software'owo emulowanej precyzji 1024 cyfr po przecinku (standard współczesnych procesorów używa, dla porównania, 16 cyfr). Dla zainteresowanych podaję użytą funkcję. Można ją wkleić w notatnik Mathematici i przetestować.


F[k_, \[Eta]_, \[Theta]_, m_, n_] := Module[{integrand, f, x}, f = Function[{z, kk, \[Eta]\[Eta], \[Theta]\[Theta]}, z^kk Sqrt[ 1 + \[Theta]\[Theta] z/2] LogisticSigmoid[\[Eta]\[Eta] - z]]; integrand = (Derivative[0, 0, m, n][f])[x, k, \[Eta], \[Theta]]; TimeConstrained[If[\[Eta] > 4, Check[ NIntegrate[Evaluate@integrand, {x, 0, \[Eta]}, Method -> "GlobalAdaptive", MinRecursion -> 13, MaxRecursion -> 64, WorkingPrecision -> 1024, PrecisionGoal -> 64], Infinity] + Check[ NIntegrate[Evaluate@integrand, {x, \[Eta], Infinity}, Method -> "GlobalAdaptive", MinRecursion -> 11, MaxRecursion -> 29, WorkingPrecision -> 1024, PrecisionGoal -> 64], Infinity], Check[ NIntegrate[Evaluate@integrand, {x, 0, Infinity}, WorkingPrecision -> 64, Method -> "DoubleExponential", MaxRecursion -> 17], Infinity] ], 600 (* 10 minutes and give UP! *), Infinity] ]

W definicji funkcji podcałkowej użyto (zgodnie z panującą obecnie modą) zamiast rozkładu Fermiego-Diraca funkcji LogisticSigmoid . Pochodne f. podcałkowej są liczone symbolicznie, a następnie całkowane (dla eta>4) w rozbiciu na dwa przedziały: 0 < x < eta oraz eta < x < Infinity algorytmem GlobalAdaptive. Obliczenie w ten sposób jednej całki trwa kilka minut. Podczas obliczeń Mathematica NIE ZGŁASZA żadnych błędów! Wszystko sugeruje, że wynik jest bezbłędny z żądaną precyzją 64 cyfr znaczących.
Czerwona krzywa została uzyskana poprzez obliczenie 2 pochodnej po eta, jej interpolację i zróżniczkowanie wielomianu interpolującego.

Kolejna krzywa, niebieska, pokazuje implementację wzoru (44) z pracy Amparo Gil et. al. (2022) , gdzie autorzy, jak twierdzą, uzyskali ,,kompletne'' rozwinięcia asymptotyczne całek Fermiego-Diraca, dla ,,dużych'' parametrów eta i theta. Rozwinięcia składają się z trzech wyrazów FR+FR+FQ, z których tylko pierwszy pokazano na wykresie. Pozostałe, jak się wydaje, tylko pogarszają sytuację. Praca nie jest dla mnie jasna, ale różniczkowanie FR po eta daje dokładność na poziomie 27 cyfr znaczących dla funkcji oraz jej pierwszej i drugiej pochodnej po eta! Jakim cudem trzecia pochodna miałaby być błędna? Nie rozumiem tego. Autorzy pracy są ekspertami w dziedzinie funkcji specjalnych, m.in. współautorami cyfrowej biblioteki NIST DLMF , zapewne wiedzą co robią znacznie lepiej ode mnie.

Kolejny rezultat, czarna przerywana linia, to wynik całkowania integratorem Arb , używającym ball-arithmetic, czyli odmiany arytmetyki interwałowej. Spodziewany wynik całkowania to w zasadzie generowany komputerowo w kilka sekund DOWÓD, polegający na oszacowaniu całki z góry i dołu. Nie licząc ewentualnych błędów w implementacji, wynik MUSI zawierać się w podanych widełkach. Jedyny punkt, gdzie można szukać ewentualnej ,,dziury w całym'' to obcięcie nieskończonego przedziału całkowania do skończonej liczby. Niemniej ,,ogon'' funkcji podcałkowej zanika wykładniczo, i można z góry określić, gdzie należy obciąć górną granicę całki aby nie dostać błędnego wyniku.

Kolejna linia (błękitna), to znane w fizyce teoretycznej rozwinięcie Sommerfelda, które powinno działać dla ,,dużego'' eta. W praktyce, eta > 68 daje tu wyniki zgodne z Arb, i są one ujemne.

Ostatnia użyta metoda to kwadratura podwójnie eksponencjalna ( Tanh-Sinh ), słynny opublikowany po japońsku algorytm, odkryty ,,u nas'' ponownie na początku XXI wieku. Jego skuteczność i prostota są legendarne: z punktu widzenia programisty jest to metoda trapezów, na dodatek bez końcowych punktów przedziału. Działa dla ,,wszystkich'' funkcji analitycznych, nic nie trzeba robić z gdy funkcja ma osobliwość na końcu przedziału. Została zaimplementowana w poczwórnej precyzji numerycznej (__float128 w C). Wynik jest zbieżny z Arb i Mathematicą na poziomie 1%.

Jakie są wnioski? Gdyby zarządzić głosowanie, ile wynosi trzecia pochodna dla eta=65, nawet w kwestii jej znaku byłyby sprzeczne opinie. Z jednej strony, proste całkowanie prostej funkcji elementarnej, szczególnie po wytoczeniu najcięższych numerycznych dział XXI wieku (quad-precision, arbitrary precision, ball-arithmetic) nie powinno dać trzech zgodnie błędnych wyników! Z drugiej strony, trzecia pochodna jest pochodną drugiej. Co prawda 2 pochodna jest niemal stałą funkcją. W zwykłej precyzji (double) dokładnie stałą, bo zmiany są na dalszych niż 16 miejscach po przecinku. Dlaczego w ogóle pochodne nie miałyby być monotoniczne? Z fizycznego punktu widzenia jest to równanie stanu zdegenerowanego gazu elektronowego, co się tam wtedy dzieje? Czy zachowanie skrajnie relatywistycznego gazu zdegenerowanego na pewno jest dobrze zrozumiane? Dla przykładu, czy masę neutrina można ot tak pominąć w analizie gwiazd o masie powyżej 50 mas Słońca i pochodzących od nich czarnych dziur? Dla przypomnienia, theta = kT/(mc^2). Temperatury podczas wybuchu supernowej sięgają 100 MeV, a masa neutrina to poniżej 1 eV (stan wiedzy na początek 2022 r.). To daje theta = 10^11. Przypadek? Nie sądzę :-)