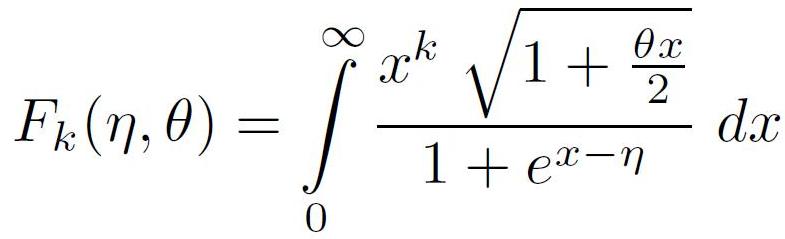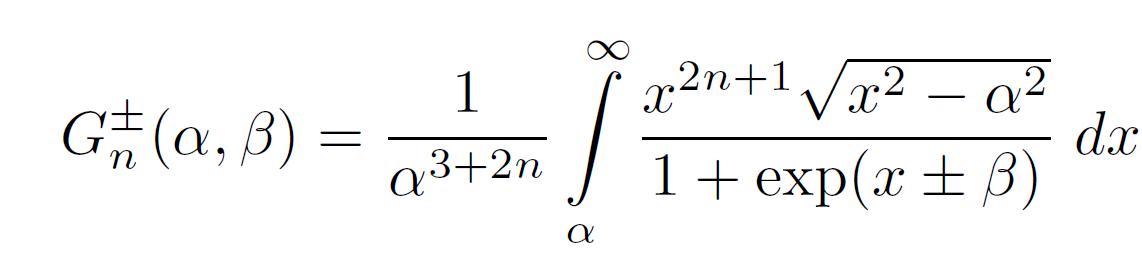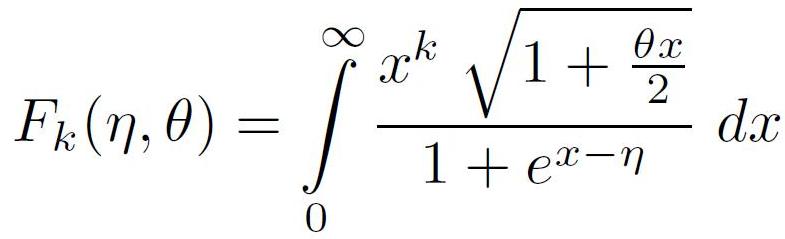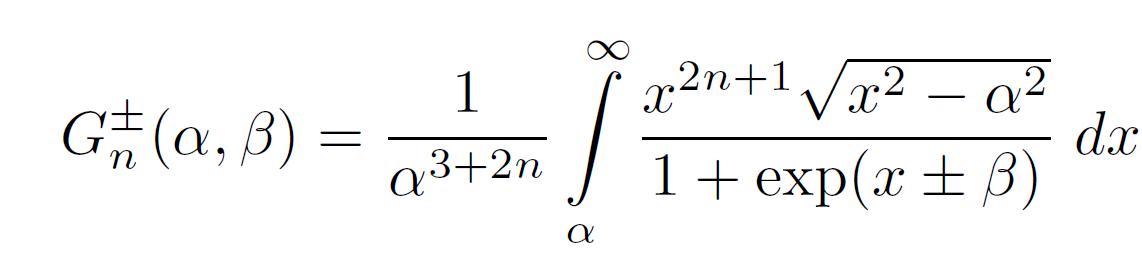Generalized Fermi-Dirac integrals

Library description

Four functions are provided:

double Ffermi(double k, double eta, double theta)
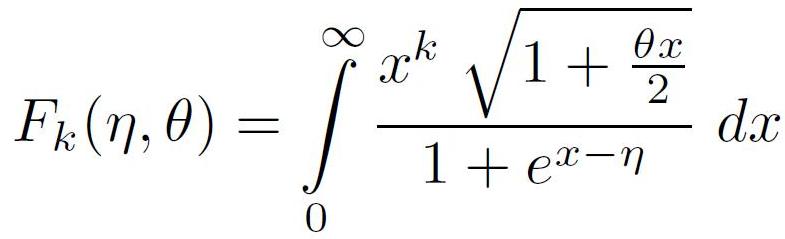
double Gfermi(double n, double alpha, double beta)
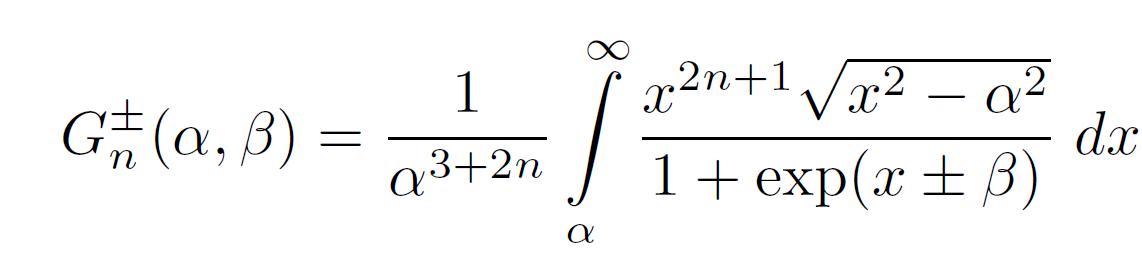
double Gp(double n, double alpha, double beta)
double Gm(double n, double alpha, double beta)

New version of the library uses Tanh-Sinh (double exponential) quadrature to compute integrals. Its performance and precision is comparable to previously used methods. Improvements are: full range of parameters, including Ffermi with k very close to -1, and arbitrary (including negative and non-integer values) n in Gfermi. Gfermi and Ffermi are independent now: multiple evaluations of Ffermi to get Gfermi is no longer problem. Extensive coverage test has been made, comparing results with arbitrary-precision results computed in Mathematica with 128-digit arithmetic and requested precision of 64 decimal places. Library is capable to get full 16-digit precision, but for extreme values of parameters very deep recursive subdivision of the integration interval are required. In typical situation (fractional k between -1/2 and 4, theta, eta up to several) parameters MAX_REXURSION=4 and ACCURACY = sqrt( DBL_EPSILON ) are enough to obtain precision of 2*DBL_EPSILON. By default MAX_RECURSION=5 and ACCURACY = pow(DBL_EPSILON,0.666) are used. This should suffice for usage in physics and astrophysics. For use as mathematical function MAX_RECURSION=8 to 16, and ACCURACY = 8 to 2 * DBL_EPSILON must be used. This should cover any Gfermi and Ffermi value representable as 64-bit float, at the expense of several times larger computational time. Experimental quickFfermi functions are provided, based on fixed abcissas and weights. They are aimed at utilization of AVX/AVX2 and might be 10 times faster than any other known to me method, if vectorization is being utilized. Previous version of the library used Fortran77 implementation of F.X.Timmes from cococubed.com .

Download

Most recent version
libfermidirac-0.28.tar.gz Updated to reflect changes in FLINT/Arb, 2024-11-12.
libfermidirac-0.27.tar.gz major upgrade, added derivatives (formulas general, but in practice work up to 3rd degree), Arb ball-arithmetic integration implemented for reference values and testing, 2022-05-29.
libfermidirac-0.26.tar.gz interface upgrade, Mathematica 12.3.1 link fixed, use in Fortran 90 and Python 3 (thx Karol U!) now possible, 2021-09-27.
libfermidirac-0.25.tar.gz minor upgrade, Mathematica 12 link fixed
libfermidirac-0.24.tar.gz major upgrade, Sommerfeld and poly-log series with hypergeometric 2F1 and Kummer U terms for extreme positive and negative chemical potentials, 2020-07-24.
libfermidirac-0.22.tar.gz minor upgrade, 2014-02-25.
libfermidirac-0.21.tar.gz , first Tanh-Sinh version, 2014-02-12.
libfermidirac-0.1.tar.gz , first version, 2012-08-02.

Installation

Standard installation procedure should work:

wget https://th.if.uj.edu.pl/~odrzywolek/homepage/codes/libfermidirac/source/libfermidirac-current.tar.gz tar -xvf libfermidirac-current.tar.gz cd libfermidirac-0.28 ./configure make sudo make install sudo ldconfig

To change default C compiler and install in home directory:

./configure --prefix=$HOME CC=icc make make install

Example of use

Go to examples/ directory where you can find example.c file:

#include <fermidirac.h> #include <stdio.h> #include <math.h> int main() { double k=4.0,result; result = Ffermi(k,1.0,1.0); printf("%lf\t%lf\n",k,result); return 0; }

If the libfermidirac library has been installed properly in system-wide location (default: /usr/local/ ), compile simply with:

gcc example.c -o example -lm -lfermidirac -lflint

and run code:

./example

with expected result:

4.000000 114.066878

In case where you install in home directory (e.g. you do not have administrator privileges, using compute cluster etc.), try:

gcc example.c -o example -I$HOME/include $HOME/lib/libfermidirac.so

and check linked libraries with ldd:

ldd example

Documentation

Report bugs to A. Odrzywolek. Code (2012-08-02) forked from PSNS to form standalone library. Simple program illustrating how to use libfermidirac is provided in doc directory, where you can also find PDF with mathematical definitions and Mathematica code used to verify accuracy. Newest version is based on double exponential quadrature with analytical (hypergeometric) expansions for both positive and negative degeneracy parameter with large absolute values.

Library should return NaN if functions are called out-of-domain, but it depends on implementation and availability of nan() function from < math.h > .

Last modified 2024-11-12 07:52