
Rozwiązanie ,,naiwne'' (i błędne): losujemy dwa kąty we współrzędnych sferycznych, a następnie obliczamy współrzędne wersora wskazującego kierunek ze wzorów na transformację wkładu sferycznego do kartezjańskiego:
x= sin(θ) sin(φ)
y=sin(θ) cos(φ)
z=cos(θ)
In[64]:=

In[47]:=
![]()
Out[47]=
![]()
Jak widać kierunki nie są całkiem losowe, ale koncentrują się na ,,biegunach'':
In[66]:=
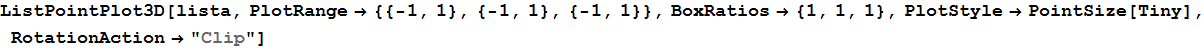
Out[66]=
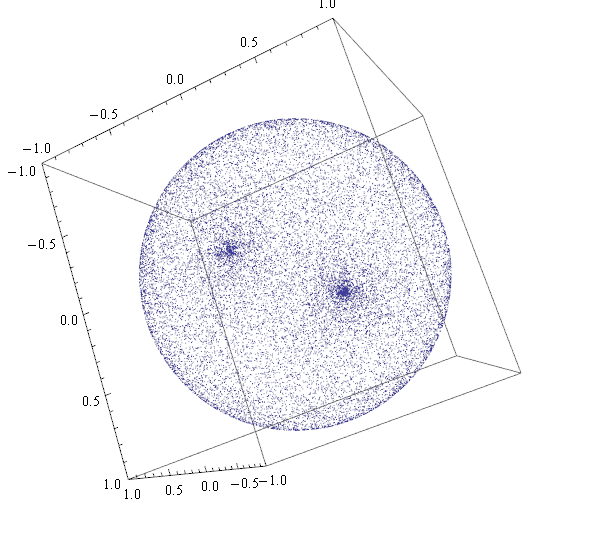
Rozwiązanie poprawne, polegające na losowaniu punktów wewnątrz sześcianu, odrzuceniu tych poza kulą, i przeskalowaniu wektora do długości 1:
In[59]:=

In[61]:=
Out[61]=
In[53]:=
![]()
Out[53]=
