x+ 6 y - 2 == 0
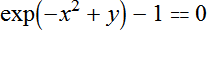
Celem zadania jest numeryczne rozwiązanie układu dwóch równań z dwiema niewiadomymi. Poniżej, jako przykład, będziemy rozwiązywać następujący układ:
x+ 6 y - 2 == 0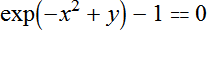
Dla wygody zapisujemy rozwiązywany układ w postaci jednej funkcji przyjmujacej jeden argument. Funkcja przyjmuje jako wartość dwuelementowy wektor (listę), i zwraca dwuelementowy wektor. Dzięki temu napisany program nie będzie różnił się zbytnio od programu rozwiązującego równania z jedną niewiadomą.
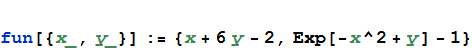
![]()
![]()
![]()
![]()
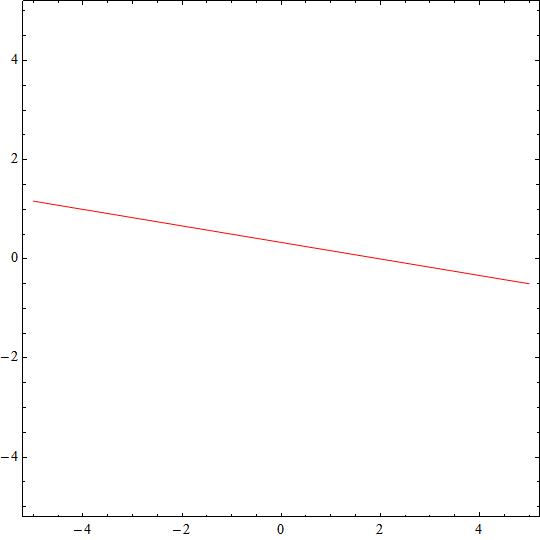
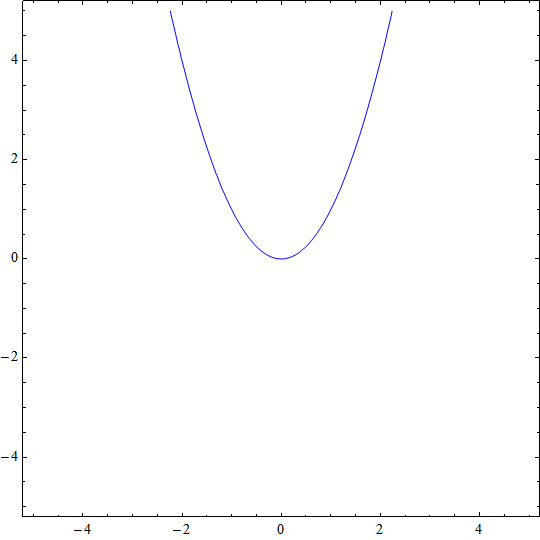
Dla wyrobienia poglądu na temat badanego układu rysujemy wykresy zadanych funkcji ( y(x) w postaci uwikłanej f(x,y)=0 ):
![]()
![]()
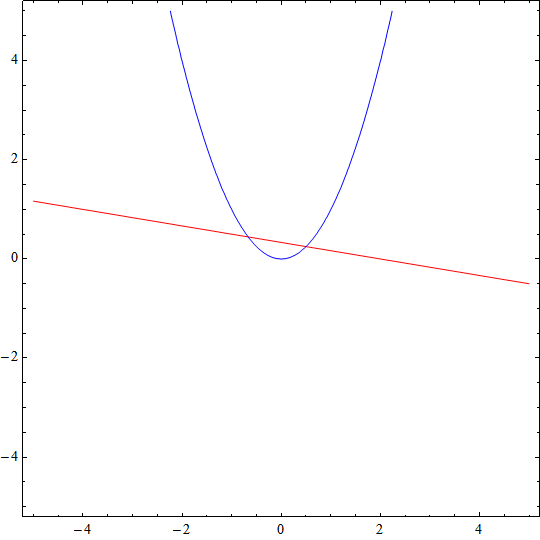
Po nałożeniu wykresy mogą (lub nie) przecinać się. Punkty przecięcia są rozwiązaniami graficznymi układu równań:
![]()
![]()
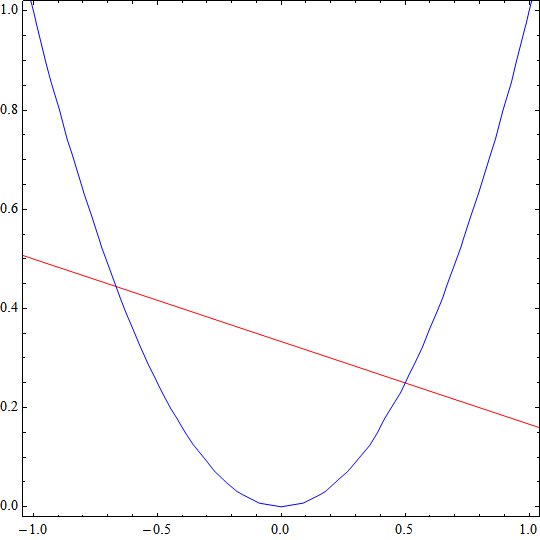
Aby rozwiązać układ numerycznie, musimy wybrać wartośc startową w pobliżu rozwiązania.
![]()
![]()
Obliczenie kolejnego przybliżenia wymaga znajomości jakobianu, czyli macierzy 2x2 zawierającej pierwsze pochodne funkcji:
![]()
![]()
Obliczamy numeryczną wartość jakobianu w wybranym punkcie:
![]()
![]()
Nowe, dokładniejsze przybliżenie otrzymujemy odejmując od poprzedniej wartości macierz odwrotną do jakobianu (Inverse) pomnożoną przez wektor zawierający wartości funkcji:
![]()
![]()
![]()
![]()
Automatycznie można to zrobić np. funkcją Nest. W tym celu tworzymy jednoargumentową funkcję obliczającą macierz odwrotną do jakobianu:
![]()
![]()
![]()
Wykorzystując funkcję Nest możemy zautomatyzować iteracje na kilka sposobów podanych poniżej:
![]()
![]()
![]()
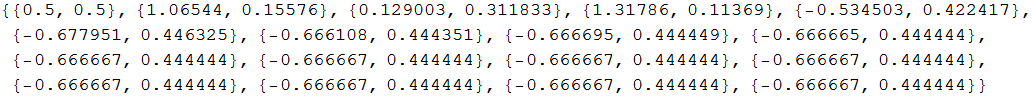

![]()
![]()

![]()
