In[64]:=
![]()
In[65]:=
![]()
In[66]:=
![]()
Out[66]=
![]()
In[67]:=
![]()
Out[67]=
![]()
In[68]:=
![]()
In[69]:=
![]()
Out[69]=
![]()
In[70]:=
![]()
Out[70]=
![]()
In[71]:=
![]()
Out[71]=
![]()
In[72]:=
![]()
Out[72]=
![]()
In[73]:=
![]()
Out[73]=
![]()
In[74]:=

Out[74]//MatrixForm=
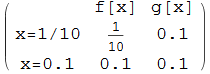
In[75]:=
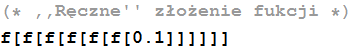
Out[75]=
![]()
In[76]:=

Out[76]=
![]()
In[77]:=
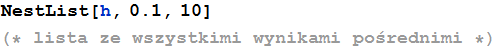
Out[77]=
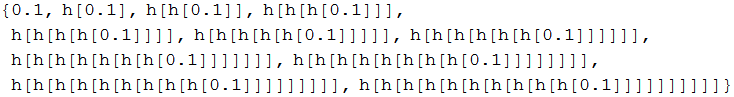
In[78]:=

Out[78]=

WNIOSEK: Liczby zmiennoprzecinkowe (nie wchodząc w szczegółowe definicje to te zawierające ,,kropkę'' dziesiętną) mają ograniczoną precyzję, i operacje na nich są obarczone błędami. Błędy te mogą ujawnić się w nieoczekiwanych sytuacjach, jak w przykładzie wyżej.
In[79]:=
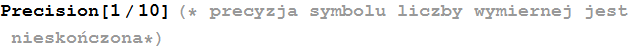
Out[79]=
![]()
In[80]:=

Out[80]=
![]()
In[81]:=

Out[81]=
![]()
In[82]:=

Out[82]=
![]()
In[83]:=
![]()
Out[83]//FullForm=
![]()
In[84]:=
![]()
Out[84]=
![]()
In[85]:=

Out[85]=
![]()
In[86]:=

Out[86]=
![]()
In[87]:=

Out[87]=
![]()
In[88]:=

Out[88]=
![]()
In[89]:=
![]()
Out[89]=
![]()