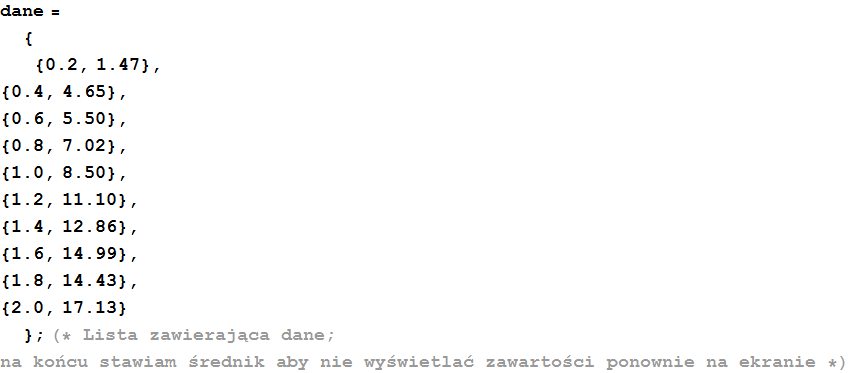
Wpisujemy lub kopiujemy z treści za pomocą Ctrl+C, Ctrl+V pomiary, wynik zapisujemy pod zmienna o dowolnej nazwie np: ,,dane’’:
In[1]:=
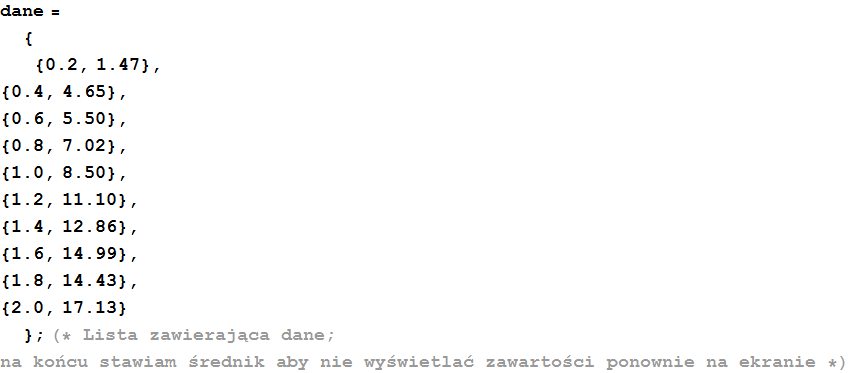
W celu wypisania na ekranie w uporządkowanej formi używamy poleceń kończących się na ,,Form’’, np:
In[2]:=
![]()
Out[2]//TableForm=
| 0.2 | 1.47 |
| 0.4 | 4.65 |
| 0.6 | 5.5 |
| 0.8 | 7.02 |
| 1. | 8.5 |
| 1.2 | 11.1 |
| 1.4 | 12.86 |
| 1.6 | 14.99 |
| 1.8 | 14.43 |
| 2. | 17.13 |
In[3]:=
![]()
Out[3]=
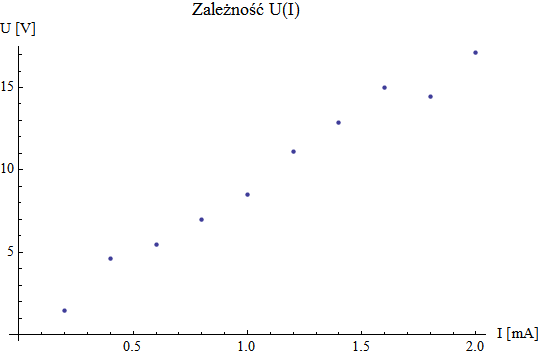
Aby narysować wykres I(U), i prad w amperach (1A =1000 mA)
Obliczam długość listy z danymi:
In[4]:=
![]()
Out[4]=
![]()
In[5]:=
![]()
Out[5]=
![]()
In[6]:=
![]()
Out[6]=
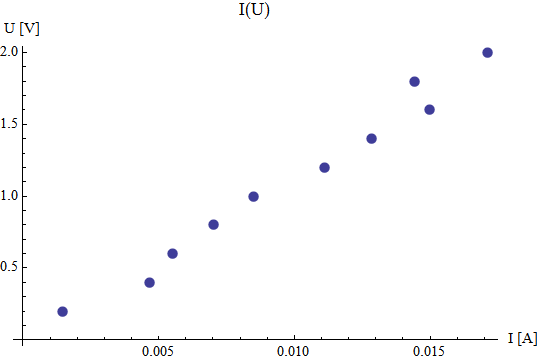
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
![]()
Niezależnie od innych metod zawsze warto zbadać problem graficznie. Używamy ,,Manipulate’’ aby ustalić wizualnie jaka wartość R wyprodukuje linie prostą najbardziej ,,pasującą’’ do punktów ,,pomiarowych’’:
In[9]:=

Out[9]=
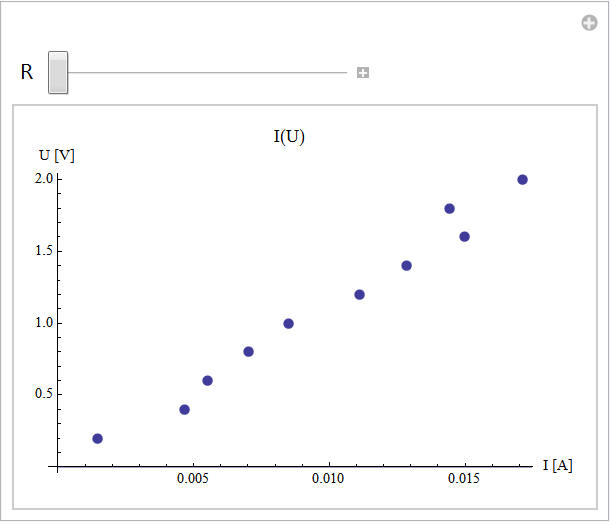
Wartość rzędu R=125 można odczytać z wykresu. Dopasowanie numeryczne wykonuje FindFit:
In[10]:=
![]()
Out[10]=
![]()
In[11]:=
![]()
Out[11]=
![]()
Bardziej szczegółowa analiza wymaga użycia bardziej wyspecjalizowanych funkcji lub napisania własnych:
In[12]:=
![]()
Out[12]=
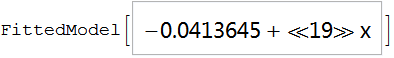
Zmienna ,,modelLiniowy’’ zawiera ogromna ilosc informacji:
In[13]:=
![]()
Out[13]=

To co moze interesowac studenta I roku fizyki:
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
In[16]:=
![]()
Out[16]=
![]()
In[17]:=
![]()
Out[17]=
| Estimate | Standard Error | t-Statistic | P-Value | |
| 1 | -0.0413645 | 0.0627433 | -0.659265 | 0.528242 |
| x | 116.883 | 5.75042 | 20.326 | 3.58765*10^^-8 |
In[18]:=

Out[18]=
![]()
In[19]:=
![]()
Out[19]=