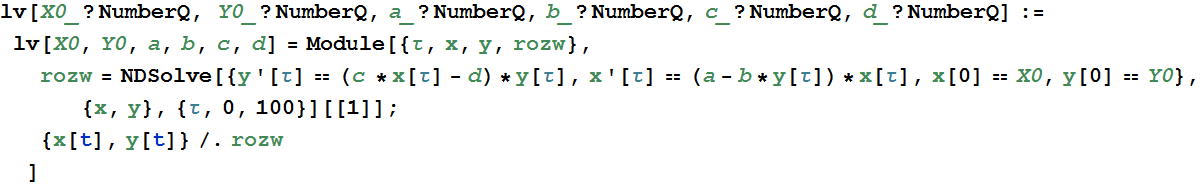
Ze względu na szybkość współczesnych procesorów, rozwiązywanie setek równań różniczkowych zwyczajnych w czasie rzeczywistym nie stanowi żadnego problemu. Dołączając do tego progranowanie dynamiczne (funkcje pamietające) możemy analizować procesy opisane skompilkowanymi układami r. różniczkowych zdyczajnych (ODE) z dziecinną łatwością. Dla przykładu podaję niżej przykład funkcji pamiętającej numeryczne rozwiązania r. Lotki-Volterry dla dowolnych parametrów i warunków początkowych:
In[1]:=
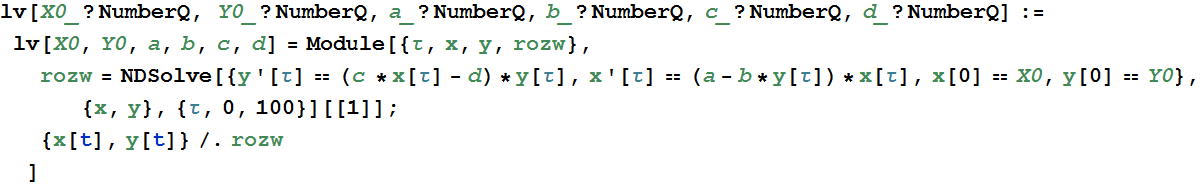
Funkcja ta generuje i zapamiętuje całe funkcje interpolujące, co jest najszybszą metodą
In[18]:=
![]()
Out[18]=
![]()
Sprawdzamy czy funkcja generuje liczby, w przeciwnym wypadku nie będzie mozna jej narysować:
In[19]:=
![]()
Out[19]=
![]()
Możemy narysować rozwiązanie dla dowolnej kombinacji sześciu parametrów:
In[20]:=
![]()
Out[20]=
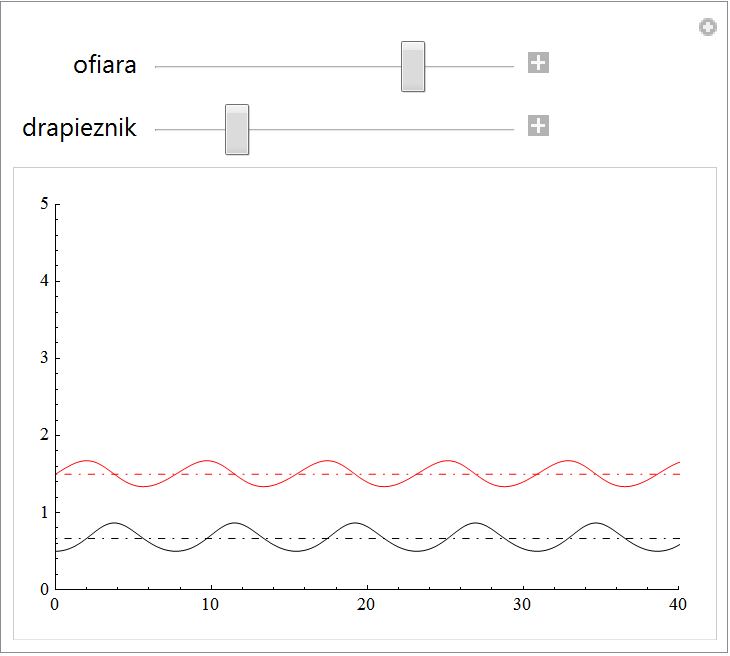
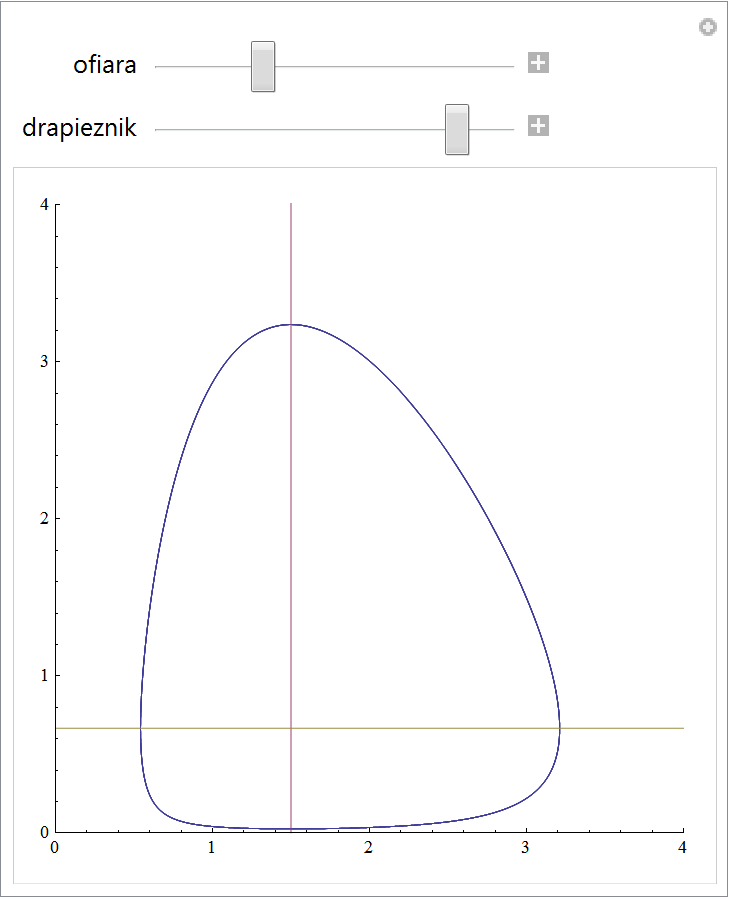
A także manipulować parametrami, np. warunkami początkowymi, obserwując jak odejście od stanu równowagi (linie przerywane) powoduje oscylacje:
In[22]:=

Out[22]=
In[28]:=

Out[28]=
In[29]:=
![]()
Out[29]=
![]()