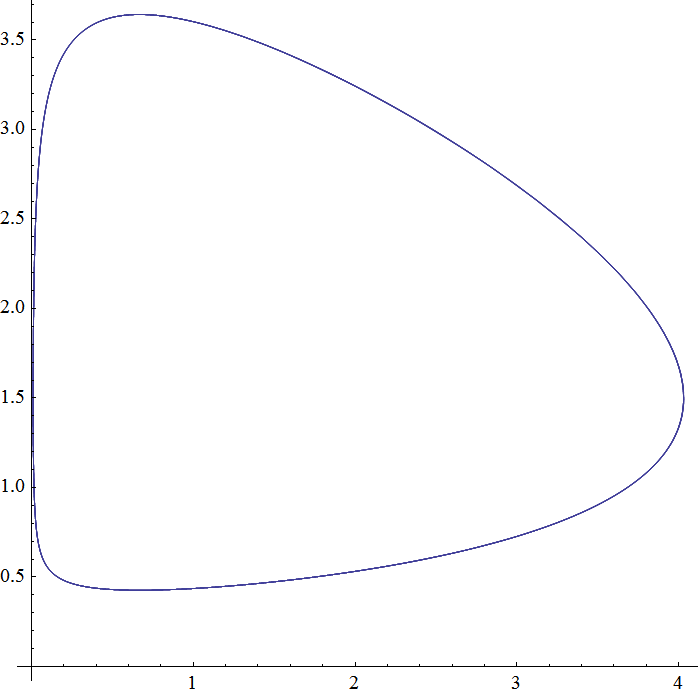
Jako przykładu numerycznej analizy układu równań różniczkowych użyję równań Lotki-Volterry (https://pl.wikipedia.org/wiki/Równanie_Lotki-Volterry).
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
Rozwiązanie w postaci funkcji specjalnych istnieje, ale nie jest użyteczne. Składnia DSolve (czyli funkcji rozwiązującej r. różniczkowe zwyczajne) jest następująca:
pierwszy argument - lista równań plus ewentualnych warunków początkowych
drugi argument - lista niewiadomych funkcji
trzeci argument - zmienna po której różniczkujemy (liczymy pochodne funkcji) [z definicji r. r. zwyczajnego jest tylko jedna taka zmienna (!) , często nie podana jawnie, np r. Lotki-Volterry można zapisać bez niej jako:
x' = (a-by)x
y' = (cx-d)y
]
In[46]:=
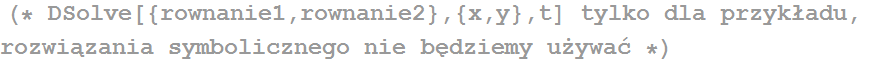
Aby rozwiązać r. r. zwyczajne numerycznie używamy NDSolve. Funkcja ta automatycznie zanalizuje podane równania i dobierze algorytm potrzebny do ich rozwiązania. Aby rozwiązać problem numerycznie wszystkie symbole oraz warunki początkowe muszą mieć przypisane wartości liczbowe, np:
In[24]:=
![]()
Out[24]=
![]()
In[25]:=
![]()
Out[25]=
![]()
In[26]:=
![]()
Out[26]=
![]()
In[27]:=
![]()
Out[27]=
![]()
Składnia NDSolve jest następująca :
argument 1 : lista równań (nie zawierająca żadnych symboli, tylko liczby !) i warunków początkowych [ {rownanie1, rownanie2, y[0] == 4, x[0] == 4/3}]
argument 2 : lista funkcji niewiadomych [ {x,y} ] lub ewentualnie [ {x[t],y[t] }
argument 3: obowiązkowy zakres zmienności zmiennej [ {t,0,100} ]
Rozwiązanie jest w postaci listy reguł transformacyjnych zawierających nowe funkcje (InterpolatingFunction) będące rozwiązaniem danego problemu (punkt krytyczny to y[0]==2/3, x[0]==3/2, im dalej od niego, tym większe wachania populacji):
In[91]:=
![]()
Out[91]=
![]()
Aby wydobyć z niego funkcje postępujemy jak podano niżej:
In[92]:=
![]()
Out[92]=
![]()
In[93]:=
![]()
Out[93]=
![]()
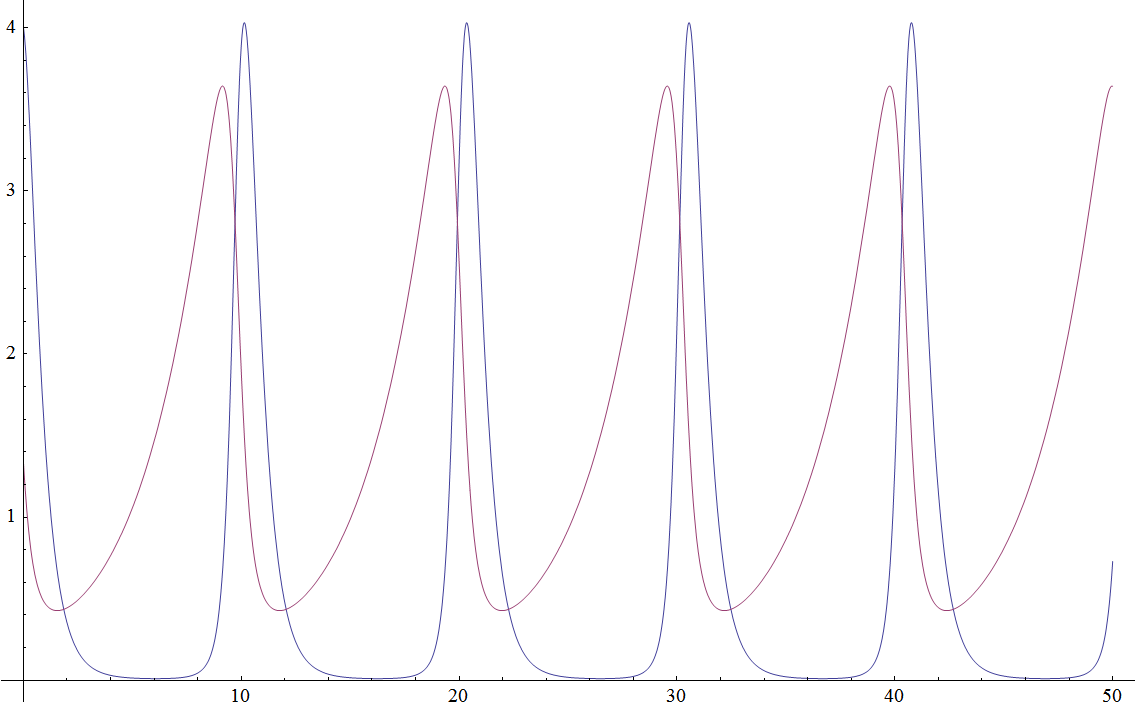
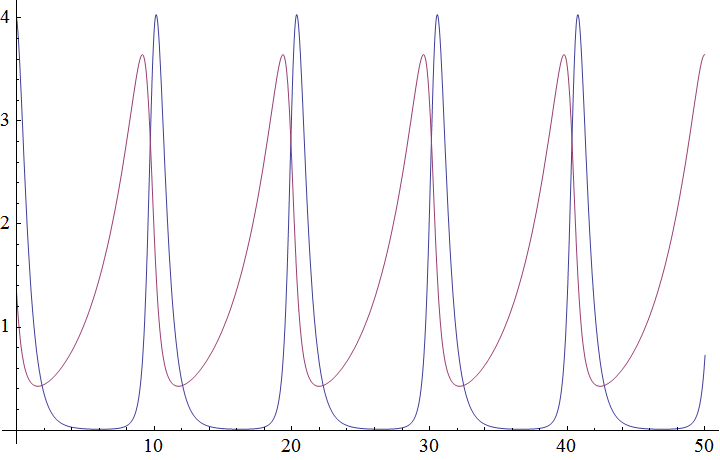
W ten sposób wyprodukowaliśmy dwie nowe funkcje: ofiara[t] i drapieżnik[t], które możemy od tego momentu używać praktycznie tak samo jak wbudowanych fukcji typu sinus, np. narysować wykresy:
In[94]:=
![]()
Out[94]=
In[95]:=
![]()
Out[95]=
In[96]:=
![]()
Out[96]=