Fundamentalnym zagadnieniem bioinformatyki (ale nie tylko) jest problem znalezienia optymalnego ułożenia dwóch lub więcej sekwencji pewnych elementów (symboli, liter, itp) . W typowym przypadku sekwencji DNA mamy do czynienia z sekwencjami czterech symboli: “C”, “G”, “T” i “A”. W przypadku sekwencji białkowych zbiorem symboli są oznaczenia (najczęściej jednoliterowe, ze względu na minimalną wielkość identyfikatorów) 20 aminokwasów, plus dodatkowe symbole jak np. “X” oznaczający nieokreślony element.
Poniżej podano 2 losowo wygenerowane sekwencje ,,DNA’’, zapisane jako zmienne o nazwach s1 i s2, które posłużą jako przykłady.

In[1]:=

In[2]:=

Out[2]=

In[3]:=

In[4]:=

Out[4]=

W najprymitywniejszej postaci, przez dopasowywanie sekwencji rozumiemy proces przesuwania jednej sekwencji względem drugiej (w sytuacji gdy zapisane są jedna pod drugą) do momentu w którym uznamy, że pewne możliwie najdłuższe fragmenty są identyczne. W najprostszych przypadkach optymalne ułożenie jest często ,,oczywiste’’. Jednak już przy próbie prostego wypisania jednej sekwekcji nad drugą natrafiamy na pierwszy problem:

In[5]:=

Out[5]//TableForm=

Otóż sekwencje które porównujemy mają na ogół inne długości, na czym więc polega porównywanie ,,nadmiarowych’’ fragmentów z ,,niczym’’? Eleganckie rozwiązanie tego zagadnienia podane zostało w pracy P. Sellersa, SIAM J. Appl. Math. 26 (787) 1974.
Po pierwsze wprowadzamy do zbioru symboli element neutralny, oznaczany zwykle w bioinformatyce jako myślnik (pozioma kreska, znak minus ,,-“).
Po drugie wprowadzamy klasę równoważności sekwencji, które różnią się tylko i wyłącznie o elementy neutralne, np: “ACGT-“, “A-C-G-T”, “------------ACGT”, “-------AC------GT--------“, są różnymi reprezentacjami tej samej sekwencji “ACGT”. W szczególności można teoretycznie przyjąć, że każda sekwencja jest formalnie nieskończonej długości, zawierając dowolnie dużo elementów neutralnych przed i za właściwą badaną sekwencją. W praktyce nie dodaje się tych elementów dowolnie dużo, a tylko tyle aby dowolne wzajemne ustawienia były możliwe. W przypadku dwóch sekwencji możemy np. rozszerzyć dłuższą z sekwencji (s1 w przykładzie) o tyle elementów neutralnych z przodu i z tyłu ile zawiera sekwencja krótsza (długość sekwencji s2).

W tym celu tworzymy funkcję o nazwie  przerwa, która zwraca łańcuch tekstowy składający się z n elementów neutralnych “-“:

In[6]:=

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Zgodnie z tym co napisałem wyżej, rozszerzam sekwencję s1 o tyle elemntów neutralnych z przodu i z tyłu ile wynosi długość sekwencji s2:

In[9]:=

Out[9]=

Aby łatwiej było manipulować sekwencjami zmieniam je na listy o nazwach s1l i s2l:

In[10]:=

Out[10]=

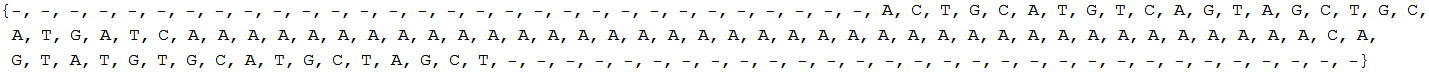
In[11]:=

Out[11]=

Poniższy mainpulator pozwala przesuwać sekwencję s1 względem sekwencji s2. Dosyć ewidentne jest, że optymalne ułożenie pojawia się w okolicy ali=60:

In[12]:=

Out[12]=

Ocenianie ,,na oko’’ może być skuteczne w najprostszych przypadkach. Liczne powody wymuszają sprecyzowanie pojęcia dopasowania:
1) ocena musi być powtarzalna
2) różne osoby (instytucje itp.) powinny mieć możliwość porównania i powtórzenia wyników
3) w przypadku długich sekwencji ocena wizualna staje się niemożliwa lub pracochłonna
4) istnieje potrzeba automatycznego dopasowywania setek i tysięcy sekwecji
5) numeryczna wartośc oceny podaje miarę jakości dopasownia
6) programy komputerowe dopasowujące sekwencje opierają się na znajdywaniu ekstremum (minimum lub maksimum) oceny w zależności od dopasowania

Konkretne numeryczne wartości które przypisujemy poszczególnym parom symboli są tematem prac naukowych. W najprostszym przykładzie poniżej przyjęto:
1) ocena wynosi 1 jeżeli symbole znajdujące się jeden nad drugim są identyczne, ale żaden z nich nie jest symbolem neutralnym
2) ocena wynosi zero, jeżeli symbole są różne, lub jeden z nich jest symbolem neutralnym

In[13]:=

In[14]:=

Out[14]=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

In[17]:=

Out[17]=

Typowym sposobem wizualizacji funkcji oceniającej jest macierz:

In[18]:=

Out[18]=

In[19]:=

Out[19]=

In[20]:=

Out[20]//MatrixForm=

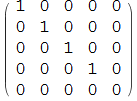
Lub w bardziej czytelnej postaci:

In[21]:=

Out[21]//TraditionalForm=

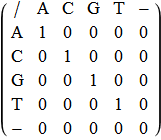
Funkcja wartosc poniżej dodaje oceny dla wszystkich mozliwych par dla sekwencji s1 i s2 przesuniętych względem siebie o ilość pozycji ali:

In[22]:=

Poniższe przykłady pokazują, że przesunięcie sekwencji s2 o 60 pozycji względem początku s1 daje znacznie wyższą wartość dopasowania niż przesunięcie o 6 pozycji. W tym właśnie sensie pierwsze ułożenie jest lepsze niż drugie. Dopasowaniem sekwencji  nazywamy takie ich  ułożenie (przesunięcie, ang. alignment) dla którego suma ocen przyjmuje największą możliwą wartość.


In[23]:=

Out[23]=

In[24]:=

Out[24]=

Aby wyznaczyć wartość przesunięcia ali dla którego sumaryczna ocena będzie maksymalna musimy zbadać wszystkie możliwe ułożenia:

In[25]:=

Out[25]=

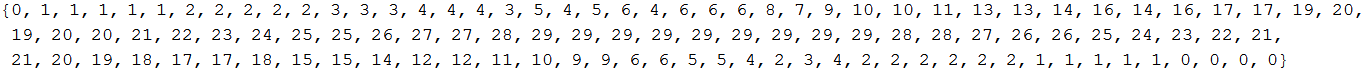
Ewidentnie, najwyższa ocena wynosi 29. Jak widać istnieje kilka dopasowań o identycznej ocenie - są one równie dobre wg. założonych kryteriów. Poniższy wykres pokazuje jak ocena początkowo rośnie, a następnie maleje:

In[26]:=

Out[26]=

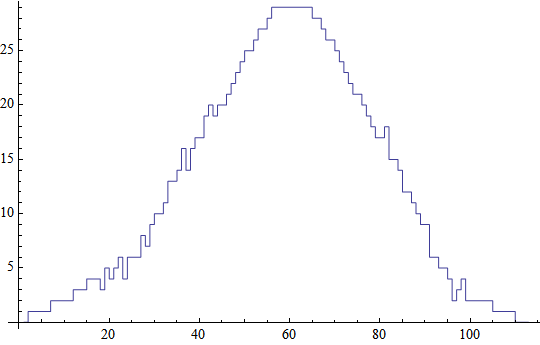
Poniższy manipulator ilustruje działanie całej procedury opisanej szczegółowo powyżej. Zachęcam do wypróbowania metody dla innych sekwencji (Uwaga: założono, że sekwencja s1 jest dłuższa niż s2).

In[27]:=

Out[27]=

Poniższe polecenie najpierw generuje wszystkie możliwe oceny w zależności od przesunięcia (Table), następnie sortuje je od najmniejszej do największej (Sort), potem odwraca (Reverse) kolejność (interesują nas najwyższe wartości, więc chcemy aby były na początku a nie na końcu). Na koniec wybieramy najlepsze, czyli pierwsze na liście (First). Pierwsza wartość podaje ocenę, druga wartość przesunięcia.

In[28]:=

Out[28]=

PODSUMOWANIE:
1) najprostszym sposobem dopasowywania sekwencji jest ich przesuwanie względem siebie
2) aby umożliwić porównywanie sekwencji o różnych długościach (a także aby wprowadzić przerwy w bardziej realistycznych metodach) wprowadzamy element neutralny (oznaczany zwykle jako “-“)
3) wszystkie sekwencje które różnią się tylko i wyłącznie o elementy neutralne (czyli po ich usunięciu stają się tożsame) traktujemy jako elementy należące do tej samej klasy równoważności; w szczególności można je traktować jako rózne ,,reprezentacje’’ tej samej sekwencji (formalnie nieskończonej, ale zawierającej skończoną ilość elementów nietrywialnych, różnych od neutralnego)
4) tworzymy (lub wybieramy gotową)  macierz podobieństwa (ang. similarity matrix, similarity rules), czyli funkcję która podaje jak oceniamy dopasowanie par elementów, uwzględniając elementy neutralne
5) obliczamy sumę ocen par elementów dla wszystkich możliwych ustawień
6) wybieramy to ustawienie, które zostało najwyżej ocenione

Algorytm opisany powyżej wymaga co obliczenia ocen jedynie w n1+ 2 n2 przypadkach, co nawet dla sekwecji o długościach rzędu tysięcy nie zajmuje komputerowi więcej niż ułamek mikrosekundy.

Bardziej realistyczne dopasowanie sekwencji wymaga wprowadzenie przerw (ang. gap), czyli elementów neutralnych nie tylko na końcach, ale także wewnątrz każdej sekwecji. Powoduje to, że ilość możliwych ustawień rośnie dramatycznie (jak bardzo?). Wymaga to radykalnej zmiany podejścia, gdyż obliczenie oceny wszystkich dopasowań jedno po drugim zajęłoby bardzo dużo czasu, przynajmniej dla dłuższych niż kilkanaście elementów sekwencji. W praktyce konieczna może też być też zmiana sposobu wartościowania elementów neutralnych, np. poprzez dodatkową karę (ang. penalty) za występujęce po sobie liczne elementy neutralne (duże przerwy). Kara ta może być zarówno dodatnia jak i ujemna.

Created with Wolfram Mathematica 7.0